Test de Rorschach

Hermann Rorschach

Hermann Rorschach(1884-1922) fue un psiquiatra suizo especializado en psicoanálisis. Es ampliamente conocido por ser el inventor del test de Rorschach, una técnica que analiza el impacto visual de ciertas imágenes en la percepción del individuo.

Según sus estudios la interpretación de imágenes ambiguas por una persona, puede desvelar rasgos de su personalidad. Con este principio desarrolló un método que se basa en mostrar manchas de tinta simétricas, en concreto 10 imágenes, 5 en blanco y negro, 2 en blanco negro y rojo, y 3 en colores variados.

Según la percepción del individuo se obtiene un patrón de personalidad fruto de la comparación de las respuestas con una extensa base de datos de resultados disponibles.

Generador de manchas

Con esta idea del test de Rorschach, hemos programado un generador aleatorio de manchas simétricas. Obtendremos en cada simulación una imagen parecida a las obtenidas por Rorschach doblando un papel con tinta china.

Como comprobareis en el programa en linea, los humanos tendemos a ver muchas caras en lo que en realidad son puras manchas hechas al azar.

Funciones

Vamos a aprovechar las funciones que creamos en el generador de islas aleatorias para crear un polígono al azar que pintaremos de negro.

Estas funciones son:

• puntomedio, que calcula el punto medio entre dos puntos dados.
• pol_cero, que crea un polígono aletorio a partir de los valores de diámetro medio y número de lados.
• div_pol, función que divide cada lado del polígono de entrada en dos y genera distorsiones caóticas aleatorias distanciando el punto medio sobre la perpendicular al lado.
• div_pol_n función recursiva que hace n veces la función anterior div_pol
• pol_cero función que llama a las anteriores y crea el polígono aleatorio
• pol_to_sf funcion que convierte un poligono en un objeto sf.

# Función punto medio
    puntomedio<-function(x1,y1,x2,y2,c_dist=0.5){
     # calcula el punto medio del lado y lo mueve
     # un porcentaje aleatorio sobre al perpendicular del lado
        xmed<-(x1+x2)/2
        ymed<-(y1+y2)/2
        # calculamos la tangente para sacar la perpendicular 
        vx<- -(y2-y1) # por anlgulos es el eje opuesto
        vy<-(x2-x1)
        # Este parametro d es importante y marca la desviación 
        # del nuevo punto respecto al lado
        d<-c_dist*runif(1,-1,1)
        # coord del nuevo punto medio final
        x0<-xmed+d*vx
        y0<-ymed+d*vy
    
        return(c(x0,y0))
    }

# Funcion divide poligono
     div_pol<-function(poligon){
             n_pol<-data.frame(x=NA,y=NA)
      # aplicamos la funión de punto medio
          for (i in 1:nrow(poligon)-1){
              n_pol<-rbind(n_pol,c(poligon[i,1],poligon[i,2]))
              n_pol<-rbind(n_pol,puntomedio(poligon[i,1],poligon[i,2],
                                          poligon[i+1,1],poligon[i+1,2]))
#              
          }
              n_pol<-rbind(n_pol,c(poligon[i+1,1],poligon[i+1,2]))
              n_pol<-na.omit(n_pol)
              return(n_pol)
  }

# Funcion recursiva de division de lados del poligono      
  div_pol_n<-function(poligon, N){
      z<-poligon
      for(i in 1:N){
          z<- div_pol(z)        
      }
      return(z)
  }
# convierte en sf un poligono dataframe  
  pol_to_sf<-function(pol,epsg=25831){
      capa <- pol %>%
        st_as_sf(coords = c("x", "y"), crs = epsg) %>%
        summarise(geometry = st_combine(geometry)) %>%
        st_cast("POLYGON")
      st_crs(capa)<-epsg
      return(capa)
  }
  
# Genera un poligono aleatorio      
    pol_cero<-function(R=10,nvert=8){
    # R= diametro medio  
    I<- R/2 # Amplitud de desviación media de irregularidades
    paso<-2*pi/nvert # mejor para para que de giro completo
    
    # creamos poligono inicial como data.frame
    pol_coord<-data.frame(x=NA,y=NA)
    a<-runif(1,0.5,10) # añadimos una funcion seno a la amplitud
    b<-runif(1,0.5,10) # añadimos otra funcion seno a la amplitud
    for(i in 1:nvert-1){
        #x<-(R+rnorm(1,I,I/3))*cos(paso*i)
        #y<-(R+rnorm(1,I,I/3))*sin(paso*i)
        x<-abs((R+I*sin(paso*i*a)+I*sin(paso*i*b)))*cos(paso*i)
        y<-abs((R+I*sin(paso*i*a)+I*sin(paso*i*b)))*sin(paso*i)
        pol_coord<-rbind(pol_coord,c(x,y))
    }
    pol_coord<-na.omit(pol_coord)
    # Añadimos al final el punto origen para cerrar el poligono
    pol_coord<-rbind(pol_coord,c(pol_coord[1,1],pol_coord[1,2]))
    return(pol_coord)
}

Tomando como base las funciones anteriores dibujaremos sobre un lienzo una mancha aleatoria usando la función pol_cero() para crear el polígono inicial.

Usaremos la funcion de dibujo plot(), pero antes indicaremos los parámetros globales del lienzo con par(), en este caso, el color del fondo y reduciremos al mínimo los márgenes.

Finalmente creamos la función mancha1() que calcula el simetro del poligono inicial y los une para devolver una forma simetrica vertical como un objeto simple features (sf). Usar objetos sf nos da acceso a todas las funciones de la librería sf, entre ellas st_area() que usaremos para limitar la salida a poligonos de cierta área y evitar resultados con poca “tinta”.

library(sf)
library(tidyverse)

# ajusto los margenes del lienzo 
par(bg=gray(0.99),oma=c(0.1,0.1,0.1,0.1),mar=c(0.1,0.1,0.1,0.1))

# funcion de mancha aleatoria
mancha1<-function(simplicidad=3,des=10){
    a=0
    while(a <150){ # esto es para evitar manchas muy chicas
        poly<-pol_cero(nvert=runif(1,4,17))
        manch<-div_pol_n(poly,simplicidad)
        #hacemos la simetrica
        manchsim<-data.frame(x=-(manch$x-des),y=manch$y)
        #convertimos a sf la mancha y su simetrica
        xy1 <- st_as_sf(manch, coords = c("x", "y"))
        xy11<-pol_to_sf(xy1)
        xy2 <- st_as_sf(manchsim, coords = c("x", "y"))
        xy21<-pol_to_sf(xy2)
        #unimos ambas
        z<-st_union(st_buffer(xy11,0.5),st_buffer(xy21,0.5))
        a<- unclass(st_area(z)) # calcula el area
    }
    return(z)
    }

# Pintamos un ejemplo
  p<-mancha1(simplicidad=runif(1,4,7),des=runif(1,15,35))
  # esto es para simplificar la forma
  # q<-st_simplify(p,preserveTopology = TRUE, dTolerance = 1)
  plot(st_geometry(p),col=gray(0.1))
  plot(st_geometry(st_buffer(p,0.2)),border=gray(0.1),add=T)
  plot(st_geometry(st_buffer(p,0.5)),border=gray(0.1),add=T)
  plot(st_geometry(st_buffer(p,-0.2)),border=gray(0.91),add=T)
  plot(st_geometry(st_buffer(p,-0.5)),border=gray(0.91),add=T)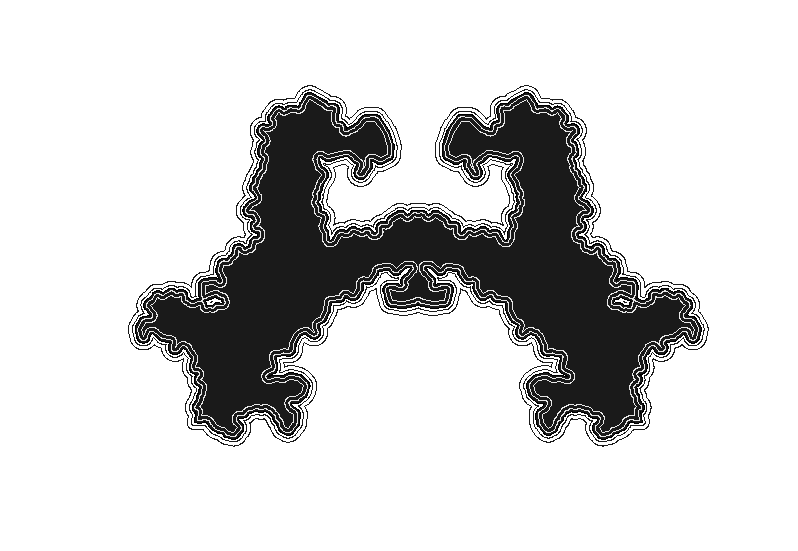

mancha del test de rorschar

Crear poligono aleatorio con Convex hull

He descubierto hace poco una manera muy sencilla de generar un polígono aleatorio geográfico usando la librería sf, que como hemos visto en otros artículos es uno de los paquetes de SIG más avanzados de R.

La función st_convex_hull calcula la envolvente convexa de un conjunto de puntos, es decir, el polígono que los encierra a todos y que pasa por los puntos.

Esto nos permite generar un polígono muy fácil, basta para ello generar unos puntos aleatorios en el plano y calcular luego la envolvente convexa de esos puntos.

Lo hemos programado en la función mancha2(), simplemente para ver su funcionamiento.

# Crea un poligono mancha con algoritmo st_convex_hull
mancha2<-function(simplicidad=3,xmax=10,ymax=20){
    a=0
    while(a <50){ # esto es para evitar manchas muy chicas
        # defino la extension del lienzo
        x<-runif(20)*xmax # limites x
        y<-runif(20)*ymax  # limite Y
        # xy aleatorio
        xy<-data.frame(x=x,y=y)
        # Convertimos a sf
        xy_sf <- st_as_sf(xy, coords = c("x", "y"))
        #creamos un poligono convexo
        poly<-st_convex_hull(st_union(xy_sf)) %>% st_cast("POINT")  %>% st_coordinates()
        # añadimos caos a los lados 
        manch<-div_pol_n(poly,simplicidad)
        #hacemos la simetrica
        manchsim<-data.frame(x=-manch$x,y=manch$y)
        #convertimos a sf la mancha y su simetrica
        xy1 <- st_as_sf(manch, coords = c("x", "y"))
            xy11<-pol_to_sf(xy1)
        xy2 <- st_as_sf(manchsim, coords = c("x", "y"))
            xy21<-pol_to_sf(xy2)
        # unimos ambas con un buffer
        z<-st_union(st_buffer(xy11,0.2),st_buffer(xy21,0.2))
        a<- unclass(st_area(z)) # calcula el area
    }
    return(z)
    }

# generamos un par de manchas de ejemplo
p<-mancha2(simplicidad=runif(1,2,4),xmax=runif(1,5,10),ymax=runif(1,10,20))
plot(st_geometry(p),col=gray(0.1))

p<-mancha2(simplicidad=runif(1,2,4),xmax=runif(1,5,10),ymax=runif(1,10,20))
plot(st_geometry(p),col=gray(0.1))

manchas tinta

Resultados

Puedes jugar en linea a interpretar estas formas aleatorias en la aplicaci´çon que he realizado aquí: programa test de Rorschach