Generador de islas aleatorias
Tras hacer el generador de ciudades me entró el gusanillo y he pensado otros talleres de programación para niños, se trata de desarrollar clases cortas como introducción a la programación de algoritmos y su aplicación directa en R.
Hablando con mi hijo mayor, pensamos que podía ser interesante crear un modelo para crear mapas de islas del tesoro… Como a mi me gustan mucho los mapas la idea me pareció genial y nos hemos puesto manos a la obra.
Muchos de los juegos de actualidad como el minecraft usan algoritmos de generación aleatoria de mapas para crear sus mundos de juego, así que es un punto que conecta muy bien con los peques actuales.
Método muy simple
Pensando cómo generar islas, creo que se nos ha ocurrido un método muy simple y en las pruebas vi que funcionaba bastante bien, así que nos lo quedamos.
Se trata de generar un polígono de n vértices a partir de un circulo simple. Lo que hacemos es añadir a la formula del círculo una irregularidad aleatoria en que se suma al radio en cada iteracción de cálculo.
Probemos, dividimos la circunferencia entera (\(2 \pi\)) en N partes, y calculamos las coordenadas de ese punto sobre la circunferencia añadiendo al radio un número aleatorio:
R=3000 # m de dario
I= 1000 # esto marca el factor de irregularidad de la cirunferecia
N=16 # el numero de puntos en que dividimos la circunferencia para representar
paso<-2*pi/N # angulo en rad de cada paso de calculo
# inicializamos una tabla de datos
coord<-data.frame(x=NA,y=NA)
# bucle de cálculo que recorre la circunferencia
for(i in 0:N-1){
x<-(R+rnorm(1,I,I))*cos(paso*i)
y<-(R+rnorm(1,I,I))*sin(paso*i)
coord<-rbind(coord,c(x,y))
}
coord<-na.omit(coord) # quitamos NA
# Añadimos el punto inicial para cerrar el poligono
coord<-rbind(coord,c(coord[1,1],coord[1,2]))
# pintamos los puntos
plot(coord,col="darkslategray",lwd=3, main="Isla aleatoria")
#pintamos el poligono
polygon(coord[,1],coord[,2],border = "burlywood4",col="bisque4")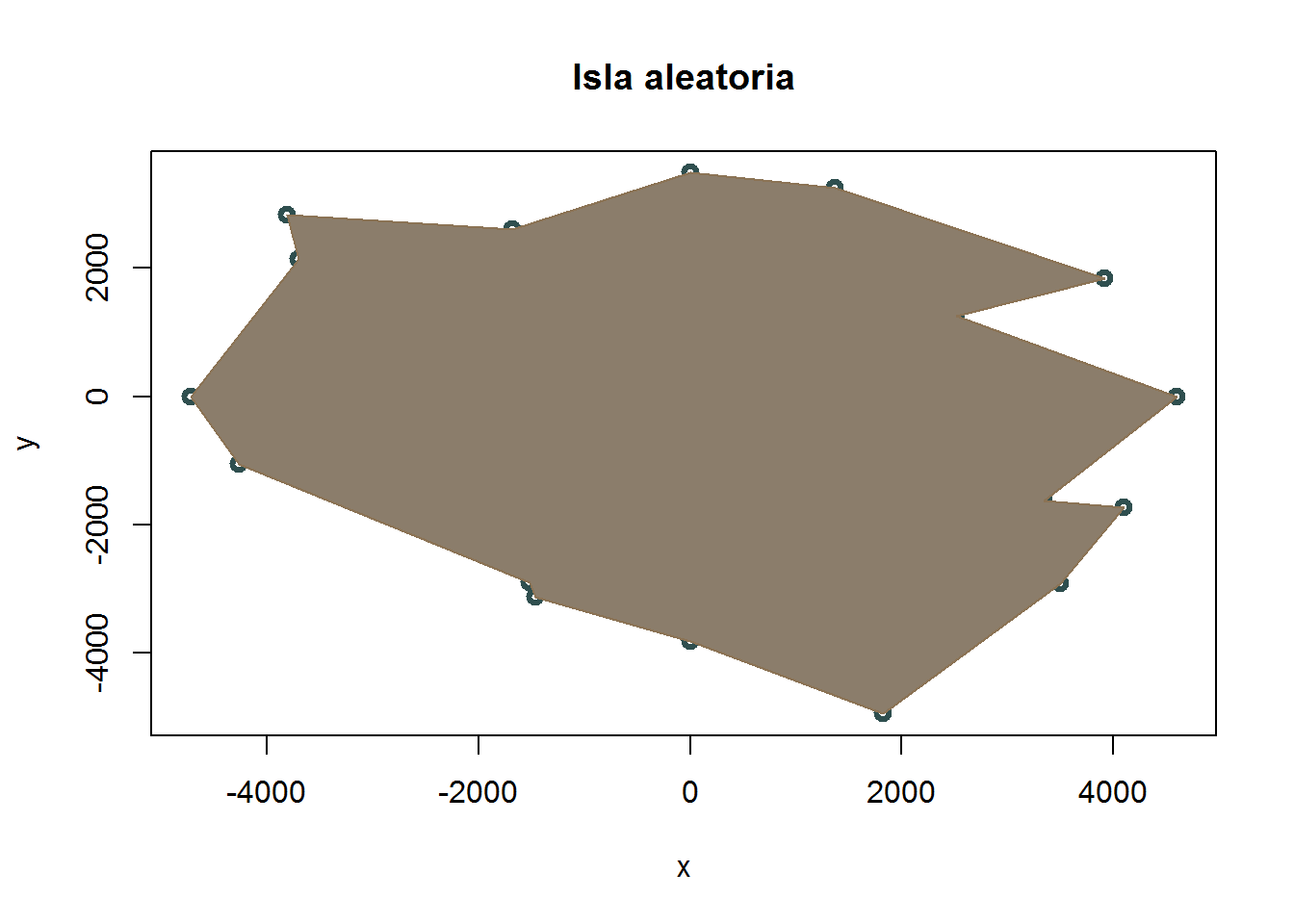
Este algoritmo genera polígonos raros, que pueden parecer islas si usamos un valor de N bajo (<20), pues si es alto las formas ya son menos realistas.
Para mejorar la apariencia, y hacer los lados más fractales, vamos a añadir un procedimiento recursivo también muy simple que aporte algo de caos sobre el contorno.
Por cierto, podemos ver una lista con los colores definidos en R aquí
Generador de caos
Sobre los polígonos generados en el punto anterior vamos a aplicar un procedimiento que nos aumente la irregularidad costera para un mayor realismo. Las costas suelen comportarse como líneas fractales, como expuso en su libro La geometría fractal de la naturaleza el matemático Mandelbrot.
Los procesos recursivos suelen dar buenos resultados así que vamos a probar una función que calcule el punto medio de cada lado del polígono isla.
Este punto medio lo desplazamos una distancia perpendicular al lado de amplitud aleatoria y formamos un nuevo polígono que divide cada lado en dos tomando un nuevo punto medio en cada uno.
Este proceso puede ser iterativo y repetirse varias veces hasta que salga una geometría singular de costa, pero eso lo haremos con otra función más adelante.
# CReamos la función punto medio
puntomedio<-function(x1,y1,x2,y2){
# calcula el punto medio del lado y lo mueve
# un porcentaje aleatorio sobre al perpendicular del lado
xmed<-(x1+x2)/2
ymed<-(y1+y2)/2
# calculamos la tangente para sacar la perpendicular
vx<- -(y2-y1) # por anlgulos es el eje opuesto
vy<-(x2-x1)
# Este parametro d es importante y marca la desviación
# del nuevo punto respecto al lado
d<-0.2*runif(1,-1,1)
# coord del nuevo punto medio final
x0<-xmed+d*vx
y0<-ymed+d*vy
return(c(x0,y0))
}
# creamos un poligono nuevo
n_pol<-data.frame(x=NA,y=NA)
# aplicamos la funión de punto medio
for (i in 1:nrow(coord)-1){
n_pol<-rbind(n_pol,c(coord[i,1],coord[i,2]))
n_pol<-rbind(n_pol,puntomedio(coord[i,1],coord[i,2],coord[i+1,1],coord[i+1,2]))
n_pol<-rbind(n_pol,c(coord[i+1,1],coord[i+1,2]))
}
n_pol<-na.omit(n_pol)
plot(n_pol,col="darkslategray",lwd=3, main="Isla aleatoria")
polygon(n_pol[,1],n_pol[,2],border = "burlywood4",col="bisque4")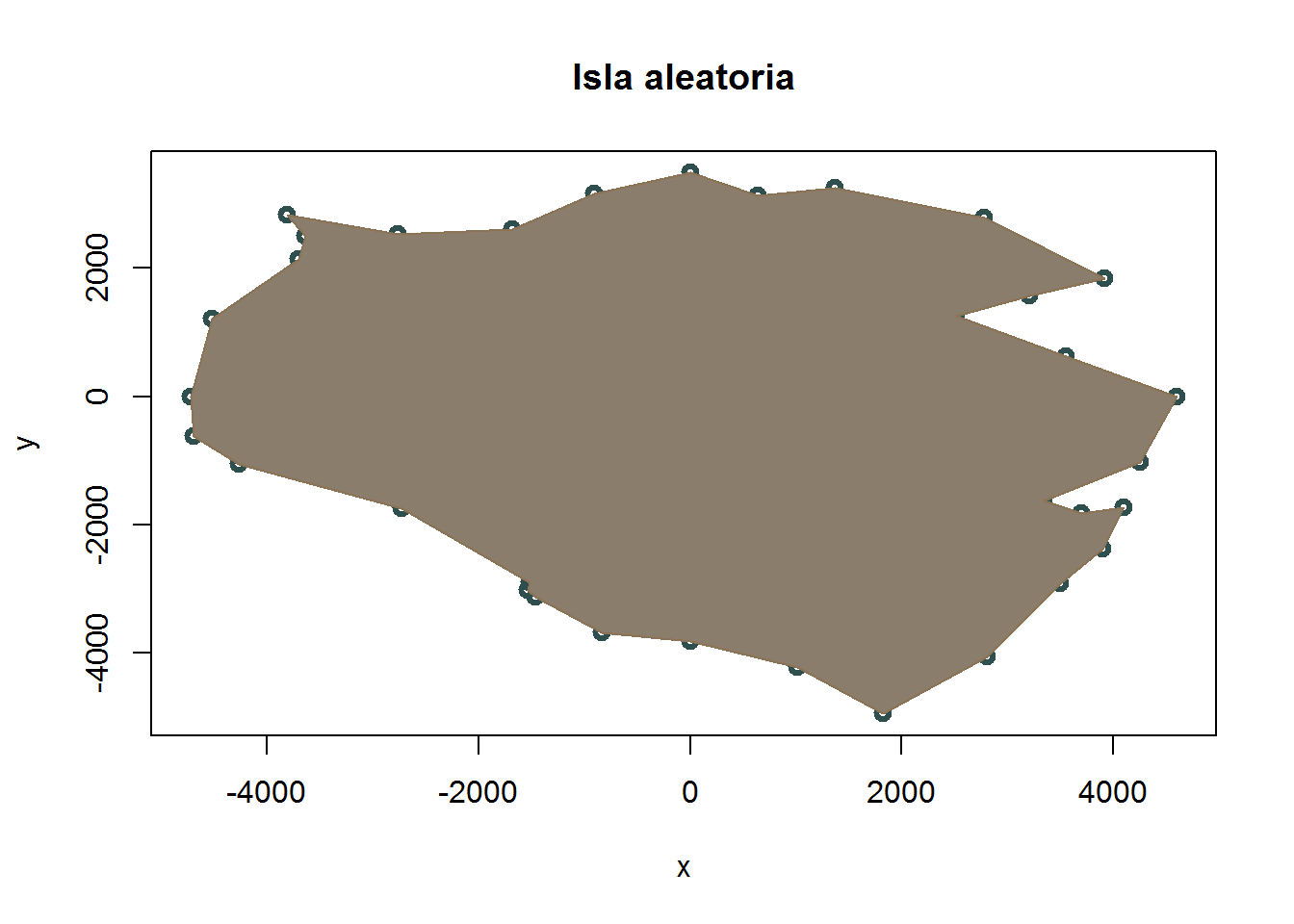
Organizar y programar el algoritmo
Hemos visto que este sistema funciona, por lo que vamos a organizar el proceso y programar una función que englobe todos los pasos y nos genere en cada llamada una nueva isla.
Crear funciones
Lo primero es definir la función que genera el polígono aleatorio inicial de isla a partir del círculo. Esta función tiene de argumentos el radio medio de la isla (del circulo creador) y el número de vértices del polígono que se genera. Llamaremos a esa función pol_cero(). Hemos hecho algunos cambios en el proceso de generación que nos han dado mejor apariencia.
Después hay que hacer una función que subdivida recursivamente cada lado del polígono en dos usando la función puntomedio() que hicimos en el paso anterior. Llamaremos a esta función div_pol() porque divide los lados y nos debe dar un nuevo polígono con más lados.
Luego necesitamos otra función que ejecute la función anterior de división del polígono de manera recursiva un número de veces N. Esta función nos dará el grado de caos de la costa y la llamaremos div_pol_n().
Finalmente para crear una isla juntaremos estas tres funciones en otra que nos simplifique la llamada final. A esta ultima función la llamaremos crea_isla().
Vamoossss a la faena:
# 1. unción que genera un primer poligono aleatorio de isla
pol_cero<-function(R=3000,nvert=5){
# R= diametro medio de la isla en m
I<- R/2 # Amplitud de desviación media de irregularidades
#N<-N # número de puntos base del boceto siempre <20
paso<-2*pi/nvert
# creamos poligono inicial como data.frame
pol_coord<-data.frame(x=NA,y=NA)
a<-runif(1,0.5,10) # añadimos una funcion seno a la amplitud
b<-runif(1,0.5,10) # añadimos otra funcion seno a la amplitud
for(i in 1:nvert-1){
#x<-(R+rnorm(1,I,I/3))*cos(paso*i)
#y<-(R+rnorm(1,I,I/3))*sin(paso*i)
x<-abs((R+I*sin(paso*i*a)+I*sin(paso*i*b)))*cos(paso*i)
y<-abs((R+I*sin(paso*i*a)+I*sin(paso*i*b)))*sin(paso*i)
pol_coord<-rbind(pol_coord,c(x,y))
}
pol_coord<-na.omit(pol_coord)
# Añadimos al final el punto origen para cerrar el poligono
pol_coord<-rbind(pol_coord,c(pol_coord[1,1],pol_coord[1,2]))
return(pol_coord)
}
#plot(pol_cero(,7),type="l")
# función que divide en 2 cada lado del poligono
# los datos de entrada deben ser un data.frame
div_pol<-function(poligon){
n_pol<-data.frame(x=NA,y=NA)
# aplicamos la funión de punto medio
for (i in 1:nrow(poligon)-1){
n_pol<-rbind(n_pol,c(poligon[i,1],poligon[i,2]))
n_pol<-rbind(n_pol,puntomedio(poligon[i,1],poligon[i,2],
poligon[i+1,1],poligon[i+1,2]))
n_pol<-rbind(n_pol,c(poligon[i+1,1],poligon[i+1,2]))
}
n_pol<-na.omit(n_pol)
return(n_pol)
}
#2. funcion recursiva
div_pol_n<-function(poligon, N){
z<-poligon
for(i in 1:N){
z<- div_pol(z)
}
return(z)
}
#plot(div_pol_n(pol_cero(,3),5),type="l")
#3. funcion final que crea y pinta una isla
crea_isla<-function(R=3000,nver=6,N=5){
#N=4
z<-pol_cero(R,nver)
z<-div_pol_n(z,N)
plot(z,col="darkslategray", cex=0.2,main=paste("Isla aleatoria: R=",R," nver=",nver," N=",N ))
# pinta fondo
polygon(c(-min(z[,1])^2,-min(z[,1])^2,max(z[,1])^2,max(z[,1])^2),c(-min(z[,2])^2,max(z[,2])^2,max(z[,2])^2,-min(z[,2])^2), col="cornflowerblue")
#Pinta la isla
polygon(z[,1],z[,2],border = "black",col="bisque4", lwd = 3)
}
# Por ultimo vemo un ejemplo
crea_isla()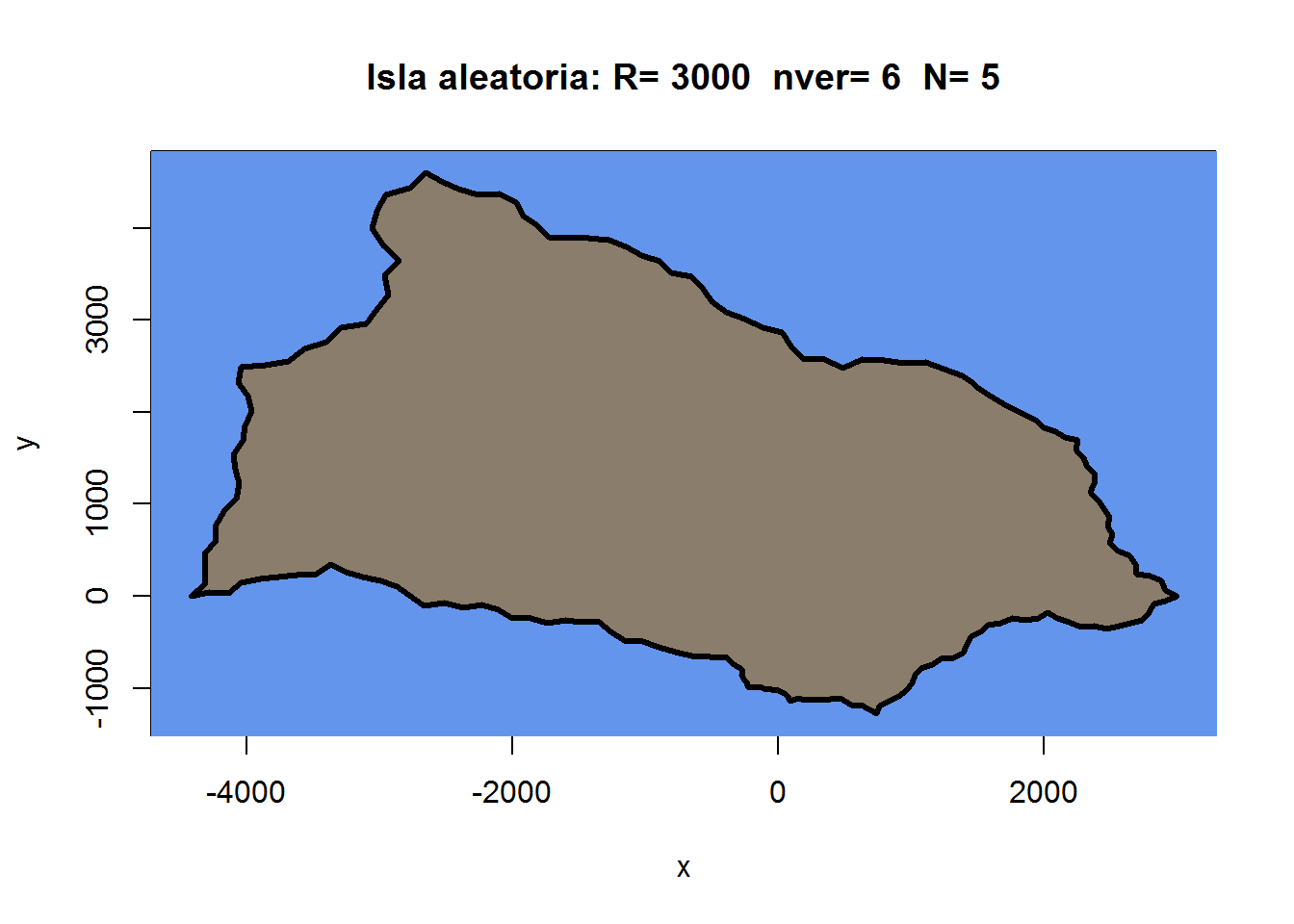
Ejemplos
Hecho el trabajo duro, vamos a probar la función y ver una muestra de resultados:
# ajusta la grafica para 6 dibujos
par(mfrow=c(3,2))
par(mar=c(0,0,0,01)+.8)
# genera 6 radios aleatorios
radio<-5000 #as.integer(rnorm(6,8000,3000))
n_pun<-as.integer(runif(6,3,15))
caos=as.integer(runif(6,3,6))
# llama a la funcion 6 veces
#sapply(radio,crea_isla,N=14)
mapply(crea_isla,R=radio,nver=n_pun,N=caos)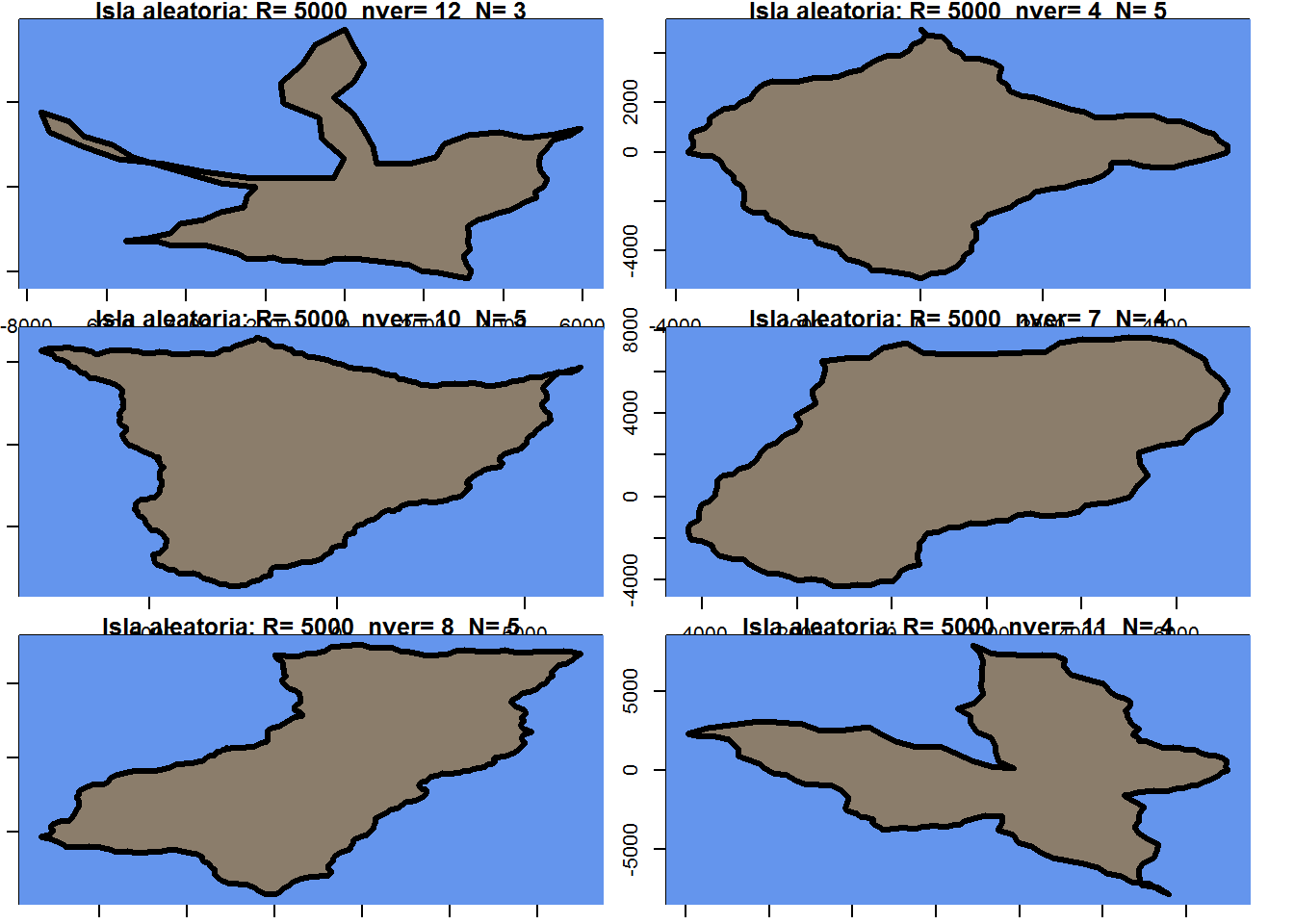
## [[1]]
## NULL
##
## [[2]]
## NULL
##
## [[3]]
## NULL
##
## [[4]]
## NULL
##
## [[5]]
## NULL
##
## [[6]]
## NULL # vuelve al modo una
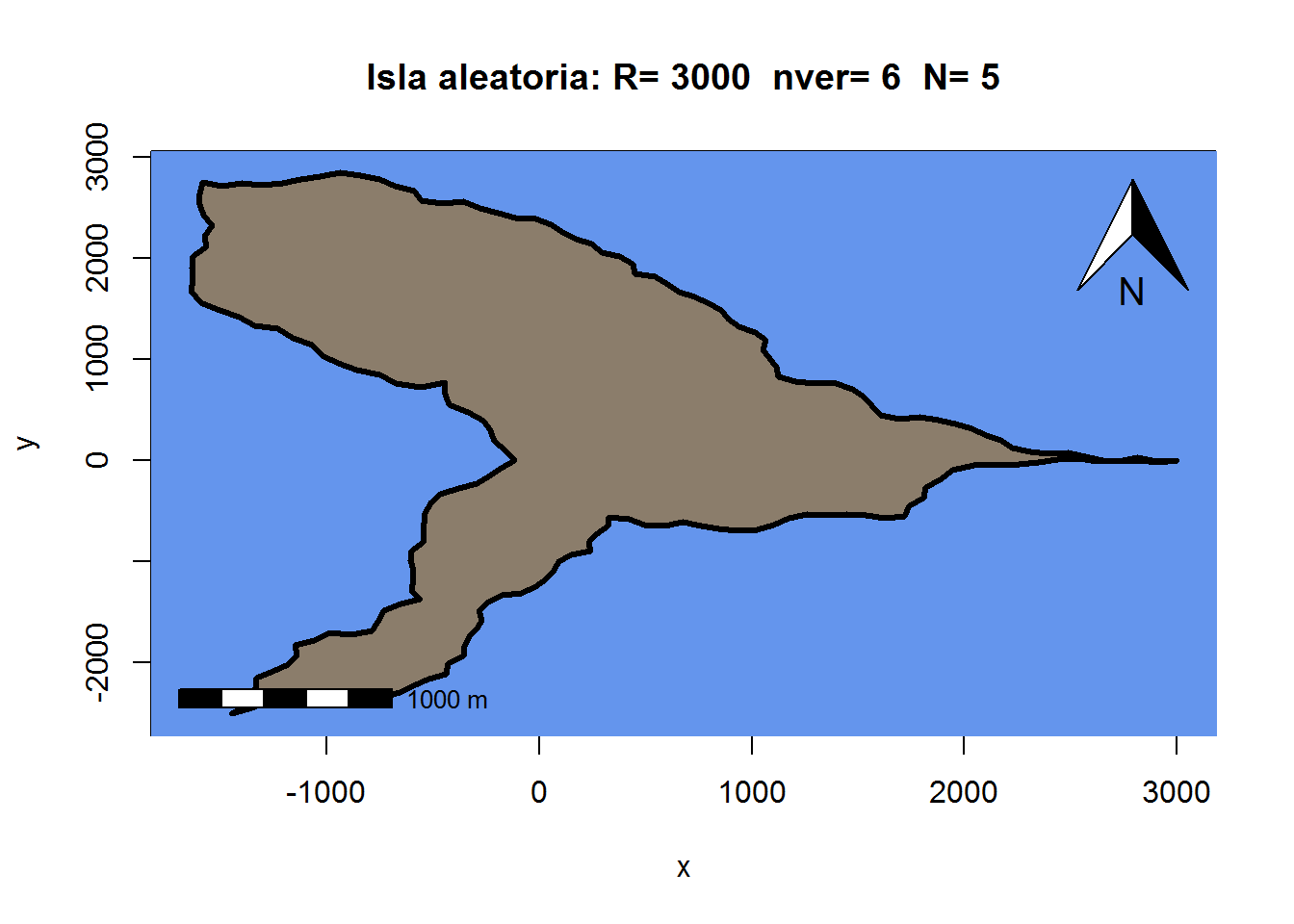
par(mfrow=c(1,1))Incluso podemos añadirle muchas cosas más al mapa, y hacer de verdad un mapa del tesoro, pero eso lo dejamos para otro día:
library(prettymapr)
crea_isla()
addscalebar()
addnortharrow(pos = "topright")