Numeros montaña
Números montaña
Aunque he tenido poco tiempo de relax este verano -los que teneis hijos sabeis de lo que hablo-,.. para el resto !disfrutad de vuestro tiempo! equivalente a 2 o tres vidas mías!!!, he leído algunas cosas interesantes y curiosas que me han mantenido en forma mental.
Una de ellas es este blog de matemáticas https://mathsedideas.blogspot.com/ en el que proponían 42 juegos matemáticos para el verano. Como os imagináis no llegué más allá de las primeras propuestas, pero me hicieron disfrutar un buen rato: aprendí la existencia de hex un juego de mesa curioso, y descubrí los números montaña, a los que vamos a dedicar hoy este artículo experimento.
Números montaña
Pues resulta que los números montaña son aquellos que al representarlos como gráfica tienen forma de montaña, es decir, que empiezan a cota baja y van subiendo hasta una cima a partir de la cual descienden de nuevo hasta la base.
Los números montaña originales son los que empiezan y terminan en 1, como el 14.721, o el 126.531, pero pueden interpretarse distintas versiones. Así los montaña generalizados son los que no empiezan o terminan en 1, sino en cualquier otro número, pero que sí mantienen la característica de subir continuamente hasta una cima y descender después, sin que el inicio y fin tengan que coincidir como el 23.620, o el 68.943, o el 456.786.421.
Pensando en estos números recordé el artículo que escribí hace unos meses Waldeinsamkeit en el que hacíamos unas gráficas con R imitando a montañas y sierras.
Objetivo
Nuestro objetivo será hacer una función en R que permita identificar si un número es o no número montaña generalizado.
El algoritmo que se me ha ocurrido después de darle unas cuantas vueltas es este, que aprovecha la función diferencia, de todas formas si se os ocurre otras forma de hacerlo, y más simple os agradecería que lo comentéis al final del post:
- Primero separamos cada cifra del número con la función
strsplitque lo transforma en una lista de caracteres individuales. - transformamos los caracteres de la lista a números y guardamos como un vector.
- Después quitamos las mesetas o duplicados de los números. Esto es algo que añadí después al ver que fallaba cuando se aplicaba la función a números con cifras repetidas como el 23.354, para esto usaremos la función
diff()que resta las cifras seguidas de la serie por lo que si es 0 indica que se repite el número, y nos vale para identificar y eliminar los valores repes de la la serie. - Calculamos el signo de cada valor de la serie
diff(), con lo que solo nos queda un valor de 1 si sube o -1 si baja en cada paso.
# Ejemplo de algoritmo para numeros montaña
num<-14821 # ejemplo de num montala
# separamos sus cifras
separa<-strsplit(as.character(num), "")[[1]]
# lo volvemos a convertir en vector número
separa<-as.integer(separa)
separa## [1] 1 4 8 2 1# calculamos diff
d_separa<-diff(separa)
d_separa## [1] 3 4 -6 -1# calculamos el signo de d_separa
signo<-sign(d_separa)
signo## [1] 1 1 -1 -1# calculamo la serie diff de signo
diff(signo)## [1] 0 -2 0- Para que sea un número montaña debe subir al principio, llegar a la cima y baja después, por lo que
sign(diff())debe ser una serie de unos (1) y luego de menos unos (-1), seguidos. La derivada dediff()es decir la diferencia de la diferencia, nos da una serie interesante, pues identifica con el valor-2las cimas como cambio de pendiente.
A la inversa los valles se identifican con el valor 2… eso para otro día.
Como buscamos los números montaña, tenemos que seleccionar solo aquellos en los que solo aparezca una cima, es decir un -2 y no varios como en el siguiente caso:
# Ejemplo de algoritmo para numeros montaña
num<-1243821
separa<-strsplit(as.character(num), "")[[1]]
separa<-as.integer(separa)
d_separa<-diff(separa)
signo<-sign(d_separa)
diff(signo)## [1] 0 -2 2 -2 0por lo que en la función tendremos que ver si como el caso anterior hay solo una cima o varias contando el número de (-2) en el vector diff(signo).
Usando estas fórmulas tenemos una manera de identificar si un número es montaña, o incluso si es valle o sierra, pero para centrarnos en los montaña vamos a crear una función que junte lo que hemos averiguado y nos dé como resultado 1 si es número montaña y 0 si no lo es.
Función que identifica un número montaña
Si unimos la descripción del proceso anterior y condensamos todo en una función obtenemos este código que sirve para detectar o identificar los números montaña generalizados:
# función para identificar los num montaña generalizados
montana<-function(x){
y<-strsplit(as.character(x), "")[[1]]
y<-as.integer(y)
quitaduplicados<-diff(y)
# me quedo sin cifras repetidas
y<-y[quitaduplicados!=0]
# derivada 2
y<-diff(sign(diff(y)))
suma<-sum(y)
negativos <- length(y[y<0])
si<-0L
if(suma < 0 & negativos == 1){si<-1L}
return(si)
}
# ejemplos
montana(133395551)## [1] 1 montana(5623)## [1] 0Ahora ya podemos calcular cuantos números montaña hay en los 10.000 primeros números naturales:
#library(purrr)
library(tidyverse)
# num montaña entre 0 y 10.000
sum(map_int(0:10000,montana))## [1] 2100Vamos a pintar algunos de ellos:
# entre:
ale<-1000:10000
# formamos un data frame con el numero y si es o no montaña
ale<-data.frame(int=ale,montana=map_int(ale,montana))
# nos quedamos solo con los montaña
solomon_ale<-ale[ale$montana==1,]
head(solomon_ale)## int montana
## 201 1200 1
## 211 1210 1
## 212 1211 1
## 221 1220 1
## 222 1221 1
## 231 1230 1 # cojemos 5 ejemplos
ejemplos<-sample(solomon_ale$int,5)
# los pinto aunque antes los transformo para poder pintarlo
# separamos las cifras
ejemplo_l<-strsplit(as.character(ejemplos), "")
a1<-map(ejemplo_l,~.x %>% as.integer())
# lo guardo como data frame para pintar
a2<- a1 %>% set_names(as.character(ejemplos)) %>% as.data.frame()
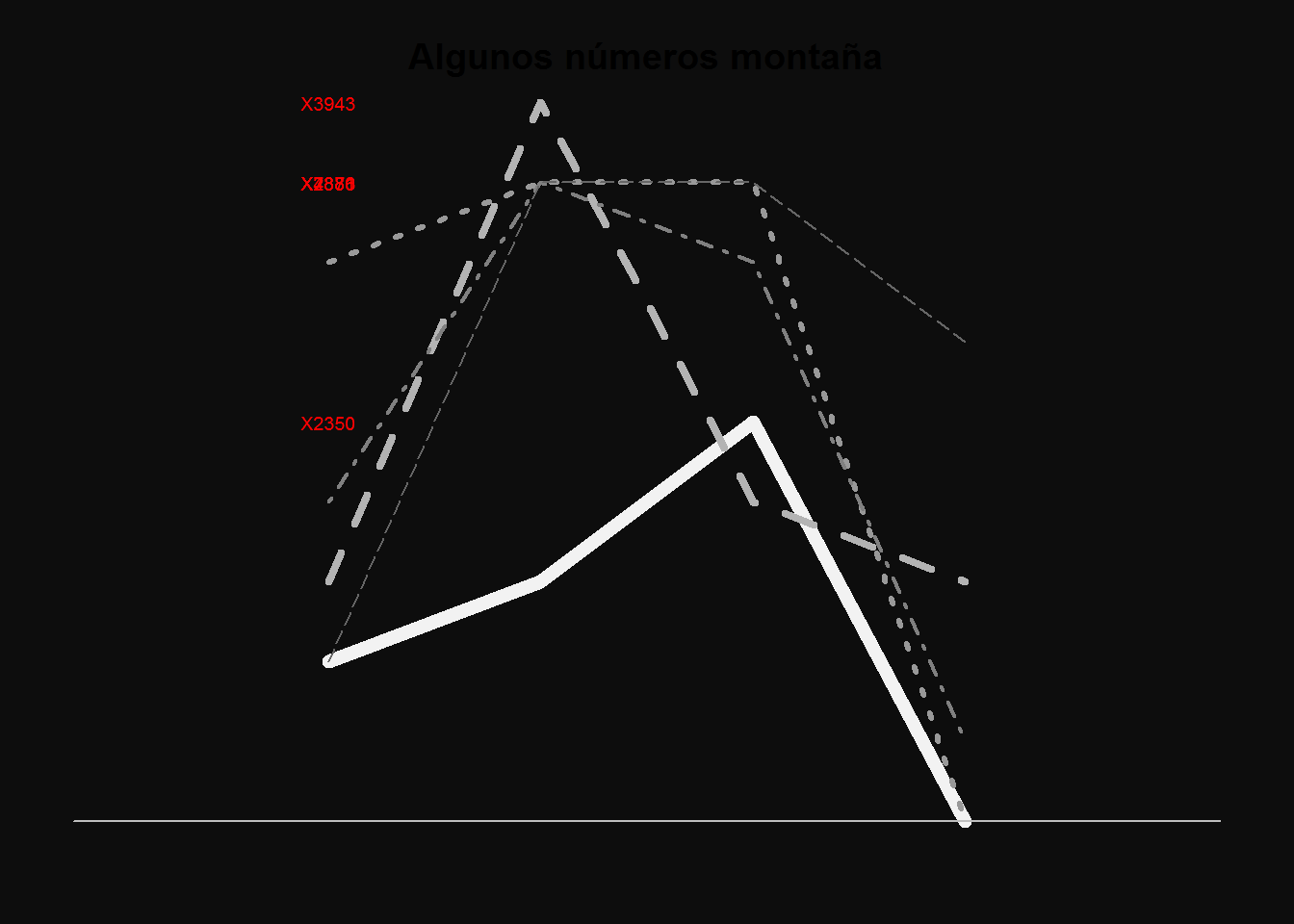
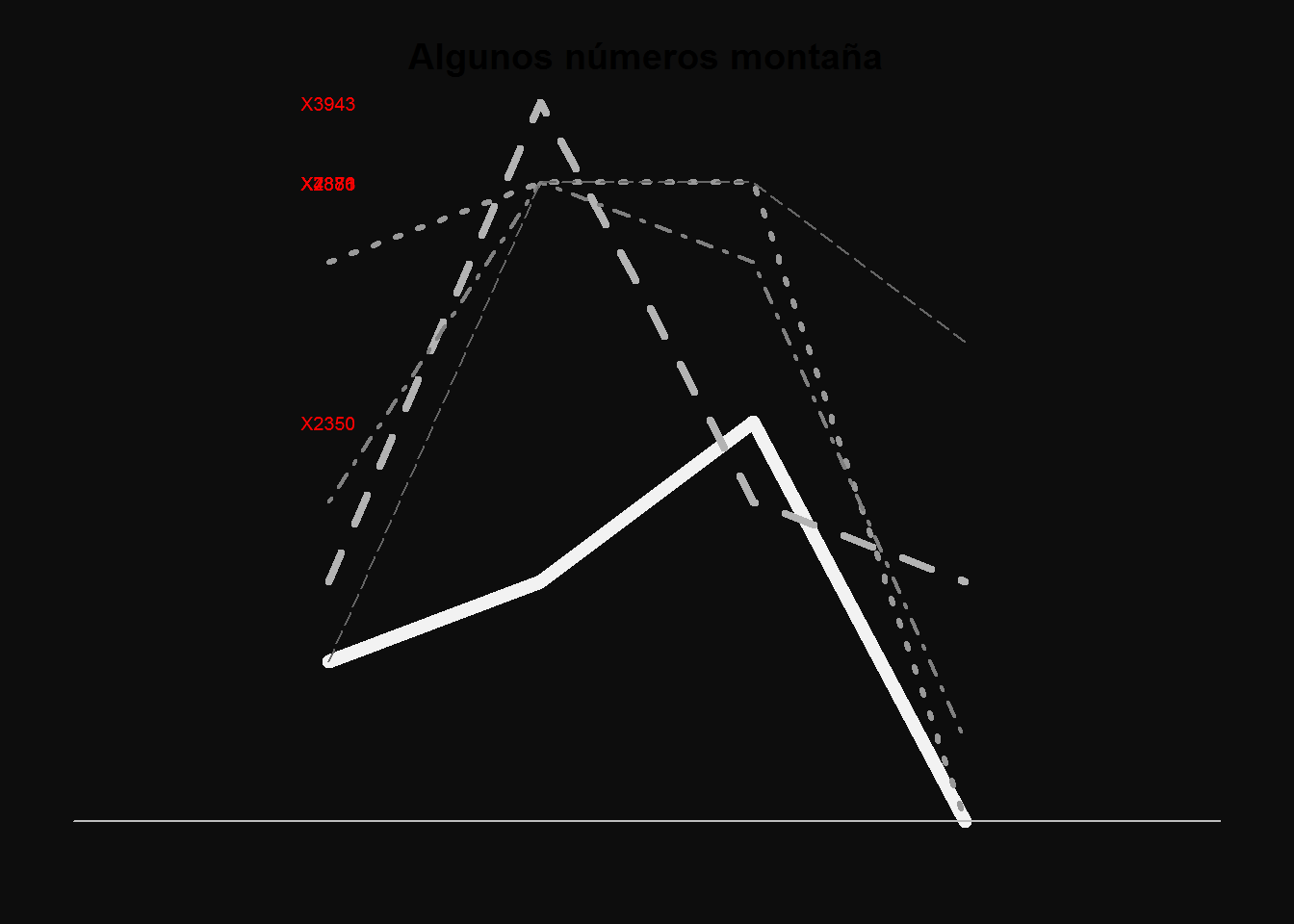
# pintamos
par(bg=gray(.05), oma=c(1,1,1,1), mar=c(1,1,1,1))
plot(a2[,1],type="l",col=gray(0.95),axes=F,
ylim=c(0,9),xlim=c(0,5),lty=1,lwd=7,
main="Algunos números montaña")
#escribimos la cifra a la izq
text(1,max(a2[,1]), colnames(a2)[1], col="red",cex=0.6)
#añadimos linea base en cero y
abline(h=0,col="grey")
for(i in 2:5){
lines(a2[,i],col=gray(0.9-i/10),lty=i,lwd=6-i)
text(1,max(a2[,i]), colnames(a2)[i], col="red",cex=0.6)
}