Manual de sf para SIG
Hace poco tiempo, usar SIG en R era bastante difícil. Teníamos que aprender el uso de muchas librerías diferentes que no tenían conexión de sintaxis. En mi caso acostumbrado a usar Arcgis y QGIS, veía que las opciones de R en aquel entonces estaban bastante limitadas, pero siempre creí que tenía un gran futuro para hacer SIG, solo faltaba tiempo de desarrollo.
La principal librería para SIG y datos espaciales era sp, pero necesitabas siempre buscar funciones complementarias en otros paquetes. Todo esto ha cambiado desde que tenemos sf. Ha sido, un acierto rehacer la programación desde la perspectiva unitaria y lógica de sf, y tener así todas las funciones SIG integradas y bajo una misma sintaxis.
La desventaja es que simple features (sf) requiere de cierta práctica para comprender su filosofía y habituarse a sus funciones, pero para eso he escrito este intenso manual de consulta de sf. El articulo es largo, pero expone un repaso fundamental de muchas de las funciones de sf y un resumen teórico que seguro os ayuda para iniciaros en la generación de mapas con R.
Indice
Simple features
La descripción de los objetos sf se ha estandarizado desde la publicación de la ISO 19125. Se trata de un documento de consenso que define la arquitectura de objetos espaciales sf (simple features) desarrollado bajo el paraguas del consorcio OpenGIS.
La base geométrica teórica la forman 4 elementos simples (subclases): el punto, la curva, la superficie y las colecciones espaciales. Las colecciones son solo listas de objetos.
OpenGIS define la arquitectura del sistema geométrico espacial así:
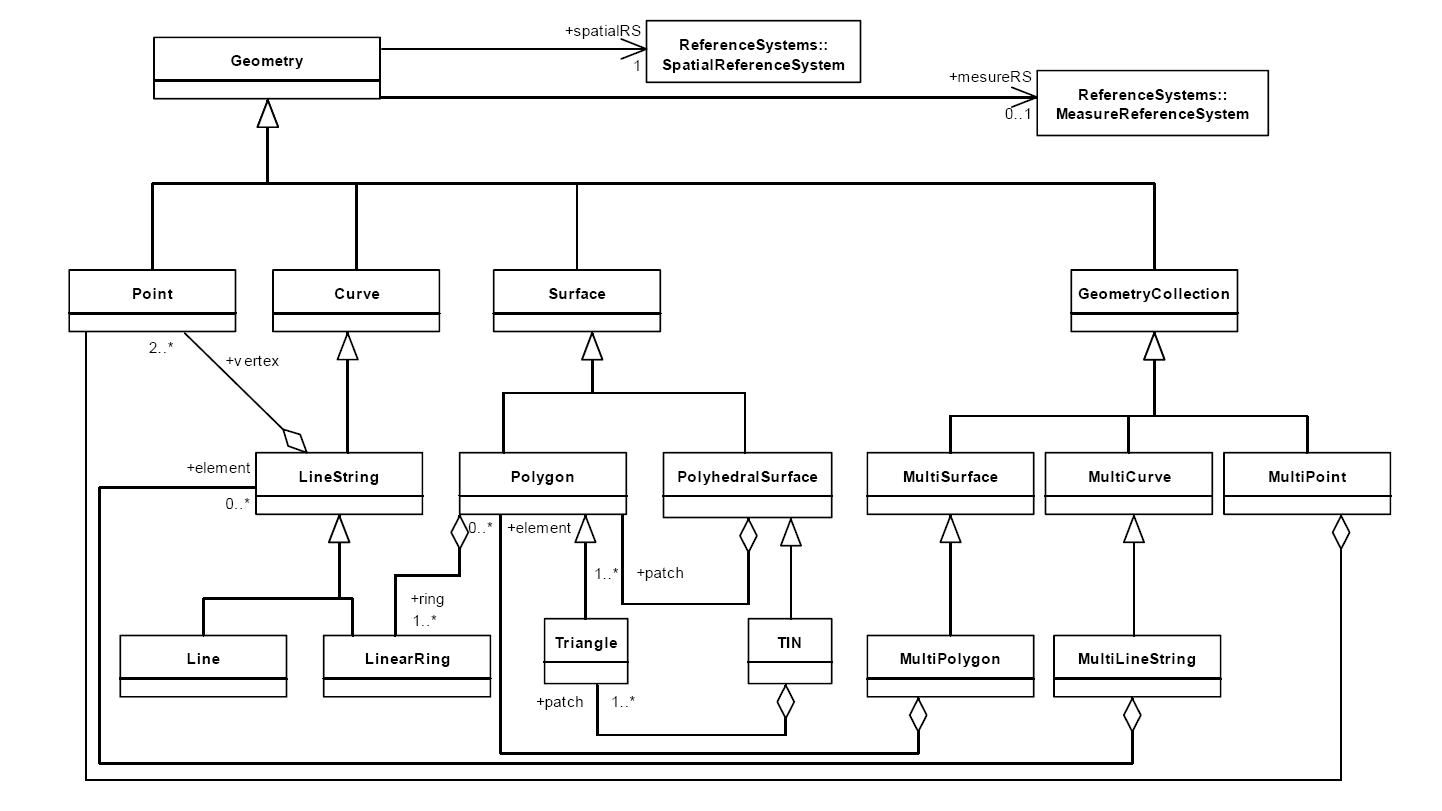
esquema OPENGIS
Como vemos, la definición geométrica es una clase, y otra diferente los sistema de referencia y medida. Esto es importante y se aplica directamente en los objetos sf, que como veremos se descomponen en otros llamados sfc y sfg.
Descomposición de sf
Los objetos sf se forman como integración de unas piezas o subclases que heredan las caracteristicas de la ISO19125.
Básicamente un objeto sf se descompone en un objeto sfc y de otro data.frame. A su vez un objeto sfc se descompone en un objeto sfg y otro CRS (sistema de coordenadas de referencia CRS). Y podemos continuar con la descomposición del sfg en otras clases como POINT, LINESTRING…
El esquema básico es así:
Veamos más detenidamente cada uno, comenzando por el de más bajo nivel hasta llegar a sf.
sfg
La clase sfg almacena la geometría con la información gráfica del objeto: las coordenadas, dimensiones, tipo de geometría… Hay 17 tipos posibles, pero los más básicos son:
- POINT: un punto simple (un vector x,y)
- MULTIPOINT: múltiples puntos (una matriz cada fila un punto)
- LINESTRING: secuencia de 2 o mas puntos conectados por lineas rectas
- MULTILINESTRING: múltiples lineas (lista de lista matrices)
- POLYGON: un polígono cerrado con cero o más huecos interiores (lista de matrices)
- MULTIPOLYGON: múltiple polígonos
- GEOMETRYCOLLECTION: cualquier combinación de los anteriores
Para crear cualquiera de estas geometrías básicas la librería sf contiene una serie de funciones creadoras:st_point(), st_multipoint(), st_linestring(), st_polygon(). Veamos unos ejemplo de uso:
library(sf)
# Crear la geometría de un punto
punto1<- st_point(c(-3.7,40.41))
punto2<- st_point(c(-2.5,39.25))
class(punto1)## [1] "XY" "POINT" "sfg" # Crea un multipunto
multip<-st_multipoint(rbind(punto1,punto2))
class(multip)## [1] "XY" "MULTIPOINT" "sfg" # Crea la geometría de una linea
linea1<- st_linestring(rbind(c(-3.7025599,40.4165001),c(2.1589899,41.3887901)))
class(linea1)## [1] "XY" "LINESTRING" "sfg"sfc
Los simple feature geometry list column o sfc son objetos sfg a los que se les aporta un sistema de referencia CRS (Coordinate Reference System). Para crear un objeto sfc se coge uno sfg y se le añade el sistema de referencia con la función st_sfc(sfg, crs). Por defecto el sistema de referencia que se añade es NA, a no ser que se especifique otro.
Un sistema de referencia se puede aportar de dos maneras, que corresponden con los 2 estandars más habituales:
- con el código EPSG
- como texto formato proj4string.
Ambos son equivalentes, pero se expresan de diferente forma. Puedes ver un listado de los códigos epsg habituales en el post geoposicionar fotografías.
También vimos en ese artículo que un sistema de referecia (CRS) se compone de varios atributos:
- Ellipsoide (describe la forma de la tierra del modelo)
- Datum (define el origen y orientación de los ejes de coordenadas)
- Proyección (pasa a 2D los datos en 3D anteriores)
Una forma de identificar la combinación de los 3 atributos anteriores es mediante los códigos EPSG llamados así por el acrónimo de European Petroleum Survey Group.
En España desde agosto del 2007 existe un sistema de referencia oficial que es el ETRS89 para la península y Baleares y el REGCAN95 para Canarias. Los códigos EPSG correspondientes a estos sistemas son:
- 4258, para coordenadas geográficas.
- 258xx, para UTM, donde “xx” es el huso (28,29,30 o 31) .
Para saber el CRS de una capa se usa la función st_crs(capa).
# Creamos una capa sfc con las geomerías sfg del ejemplo anterior
coleccion<-st_sfc(punto1, linea1, crs = 4326)
class(coleccion)## [1] "sfc_GEOMETRY" "sfc" st_crs(coleccion)## Coordinate Reference System:
## EPSG: 4326
## proj4string: "+proj=longlat +datum=WGS84 +no_defs" coleccion## Geometry set for 2 features
## geometry type: GEOMETRY
## dimension: XY
## bbox: xmin: -3.70256 ymin: 40.41 xmax: 2.15899 ymax: 41.38879
## epsg (SRID): 4326
## proj4string: +proj=longlat +datum=WGS84 +no_defssf
Cuando, a un objeto sfc le asociamos un data.frame obtenemos un objeto sf.
Para crear una instancia de sf está la función st_sf(data.frame, sfc)
# Creamos una data frame
data <- data.frame(nombre = c("punto", "Linea"))
objeto_sf<- st_sf(data, coleccion)
class(objeto_sf)## [1] "sf" "data.frame" objeto_sf## Simple feature collection with 2 features and 1 field
## geometry type: GEOMETRY
## dimension: XY
## bbox: xmin: -3.70256 ymin: 40.41 xmax: 2.15899 ymax: 41.38879
## epsg (SRID): 4326
## proj4string: +proj=longlat +datum=WGS84 +no_defs
## nombre coleccion
## 1 punto POINT (-3.7 40.41)
## 2 Linea LINESTRING (-3.70256 40.416... # para descomponer y quedarnos solo con data.frama
st_set_geometry(objeto_sf,NULL)## nombre
## 1 punto
## 2 Linea # para descomponer y quedarnos solo la geometría
st_geometry(objeto_sf)## Geometry set for 2 features
## geometry type: GEOMETRY
## dimension: XY
## bbox: xmin: -3.70256 ymin: 40.41 xmax: 2.15899 ymax: 41.38879
## epsg (SRID): 4326
## proj4string: +proj=longlat +datum=WGS84 +no_defsLectura-Escritura
Lectura
La función de lectura básica de sf es st_read(). Esta función lee múltiples formatos de datos SIG.
Vamos a hacer un ejemplo leyendo los datos shp descargados de la web del Ministerio de Medio Ambiente de España
Descargamos la capa de las comunidades autónomas de la web (Comunidades autonomas.shp) y la guardamos en la carpeta capas.
# Lectura de datos
library(sf)
# Leemos capa autonomías
autonomias <- st_read("../../static/capas/Comunidades autonomas.shp")## Reading layer `Comunidades autonomas' from data source `C:\R\publicaciones\enrdados\static\capas\Comunidades autonomas.shp' using driver `ESRI Shapefile'
## Simple feature collection with 19 features and 3 fields
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -18.16122 ymin: 27.63779 xmax: 4.327785 ymax: 43.79238
## epsg (SRID): NA
## proj4string: +proj=longlat +ellps=GRS80 +no_defs class(autonomias)## [1] "sf" "data.frame" # pintamos la geometría de la capa
plot(st_geometry(autonomias))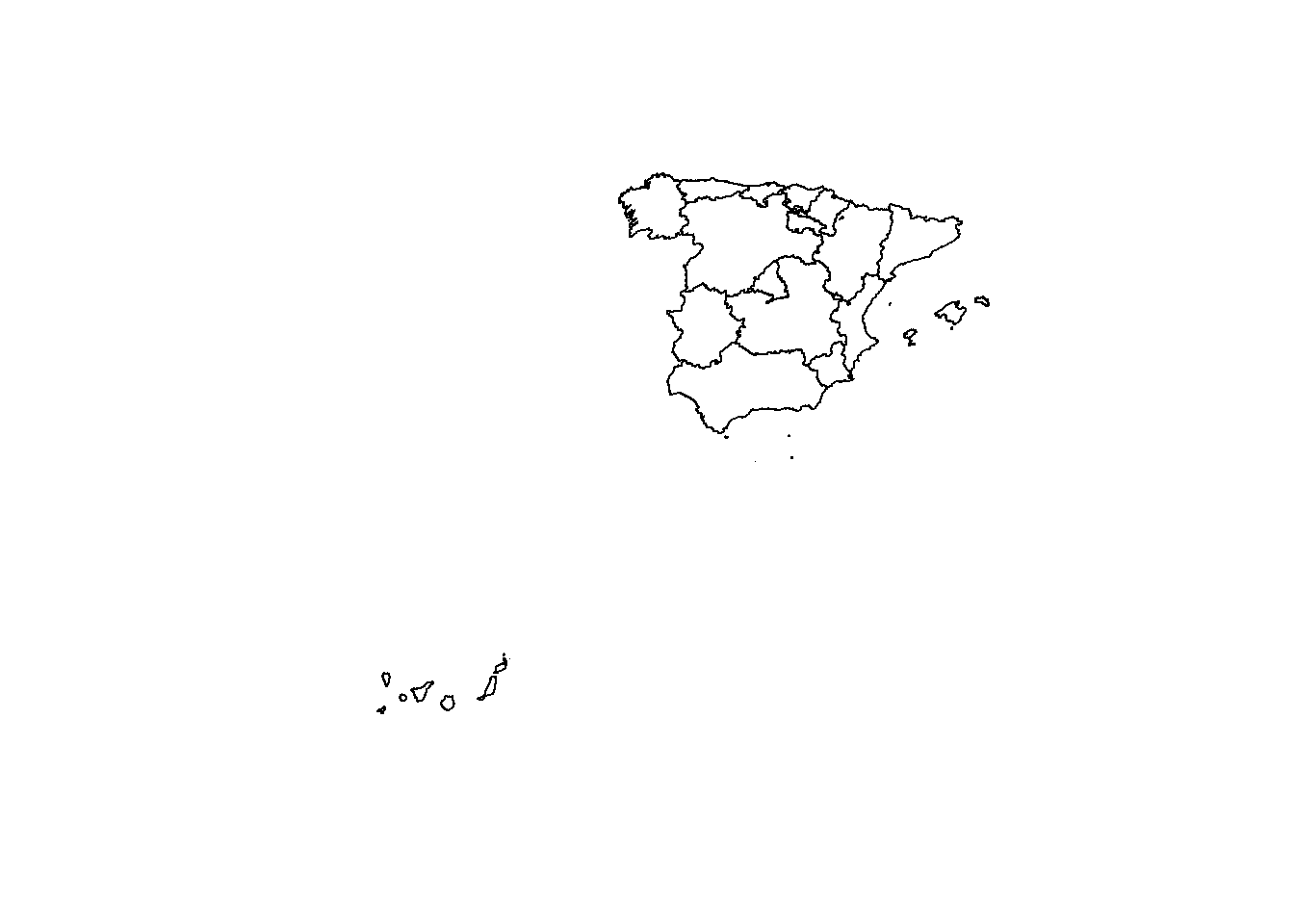
head(autonomias)## Simple feature collection with 6 features and 3 fields
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -18.16122 ymin: 27.63779 xmax: 4.327785 ymax: 43.51369
## epsg (SRID): NA
## proj4string: +proj=longlat +ellps=GRS80 +no_defs
## COD_CCAA NOML_CCAA NOM_CCAA
## 1 01 COMUNIDAD AUTONOMA DE ANDALUCIA ANDALUCIA
## 2 02 COMUNIDAD AUTONOMA DE ARAGON ARAGON
## 3 03 COMUNIDAD AUTONOMA DE LAS ILLES BALEARS BALEARES
## 4 04 COMUNIDAD AUTONOMA DE CANARIAS CANARIAS
## 5 05 COMUNIDAD AUTONOMA DE CANTABRIA CANTABRIA
## 6 06 COMUNIDAD AUTONOMA DE CASTILLA-LA MANCHA CASTILLA-LA MANCHA
## geometry
## 1 MULTIPOLYGON (((-5.035409 3...
## 2 MULTIPOLYGON (((-0.747266 4...
## 3 MULTIPOLYGON (((3.213645 39...
## 4 MULTIPOLYGON (((-16.15754 2...
## 5 MULTIPOLYGON (((-3.590244 4...
## 6 MULTIPOLYGON (((-2.901019 4...Escritura
Para escribir usaremos la función st_write() que tiene muchas opciones de formato.
# guarda la capa como ccaa.shp
st_write(autonomias, "ccaa.shp", delete_layer = TRUE) # overwrites
# En formato csv también con as coordenadas de la capa
st_write(pts2, "pts.csv", layer_options = "GEOMETRY=AS_XY")Selección
Seleccion por tabla
Los objetos sf, son por tanto geometrías asociadas a tablas, y podemos usar los mismos criterios de selección que utilizamos en los data frames.
Una vez que hemos leído la capa como sf, además de la geometría contiene datos asociados como data.frame. Estos datos se pueden seleccionar como si se tratase de una data.frame normal y corriente:
Usaremos en este ejemplo dplyr. Para seleccionar del mapa de CCAA todas menos Canarias.
library(dplyr)
# vemos las variables que tiene la capa (la geometría es una de ellas)
class(autonomias)## [1] "sf" "data.frame" summary(autonomias)## COD_CCAA NOML_CCAA NOM_CCAA
## 01 : 1 CIUDAD DE CEUTA : 1 ANDALUCIA: 1
## 02 : 1 CIUDAD DE MELILLA : 1 ARAGON : 1
## 03 : 1 COMUNIDAD AUTONOMA DE ANDALUCIA: 1 ASTURIAS : 1
## 04 : 1 COMUNIDAD AUTONOMA DE ARAGON : 1 BALEARES : 1
## 05 : 1 COMUNIDAD AUTONOMA DE CANARIAS : 1 CANARIAS : 1
## 06 : 1 COMUNIDAD AUTONOMA DE CANTABRIA: 1 CANTABRIA: 1
## (Other):13 (Other) :13 (Other) :13
## geometry
## MULTIPOLYGON :19
## epsg:NA : 0
## +proj=long...: 0
##
##
##
## head(autonomias$NOM_CCAA)## [1] ANDALUCIA ARAGON BALEARES
## [4] CANARIAS CANTABRIA CASTILLA-LA MANCHA
## 19 Levels: ANDALUCIA ARAGON ASTURIAS BALEARES CANARIAS ... VALENCIA ## seleccion
# todas las CCAA menos Canarias
autonomias %>% select(COD_CCAA)%>% filter(COD_CCAA!="04") %>% plot()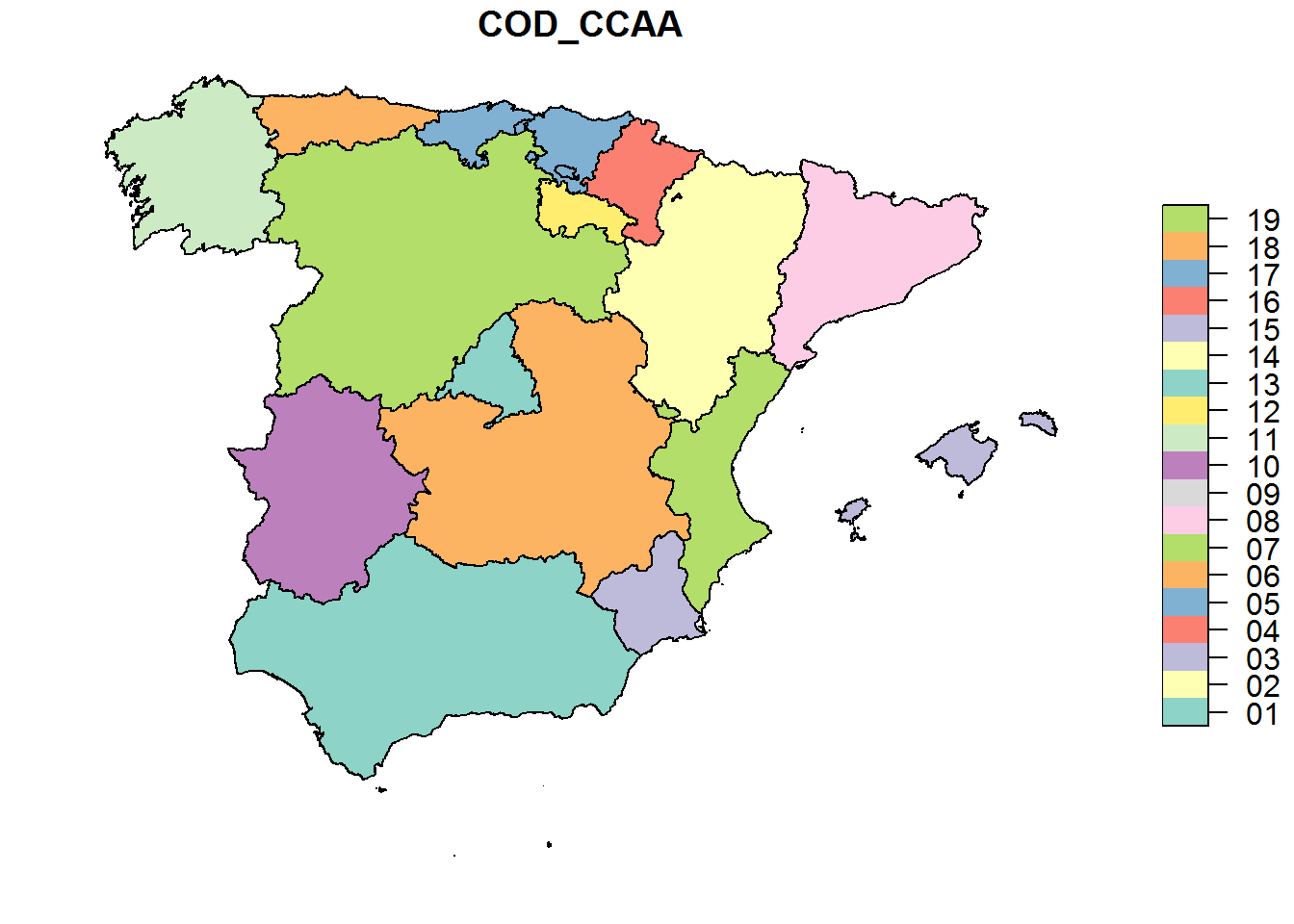
# Canarias sola
autonomias %>% select(COD_CCAA)%>% filter(COD_CCAA=="04") %>% plot()
Seleccion espacial
Además de usar criterios de seleccion de tabla, las geometrías permiten seleccionar por criterios de posición como: contacto, inclusión, igualdad, contenido en, etc.
Murcia<-autonomias %>% select(COD_CCAA)%>% filter(COD_CCAA=="15")
# selecciono las ccaa que tocan el borde de Murcia
toca_murcia<-autonomias[Murcia, op = st_touches]
# pinto el resultado
plot(st_geometry(toca_murcia),col=5:8)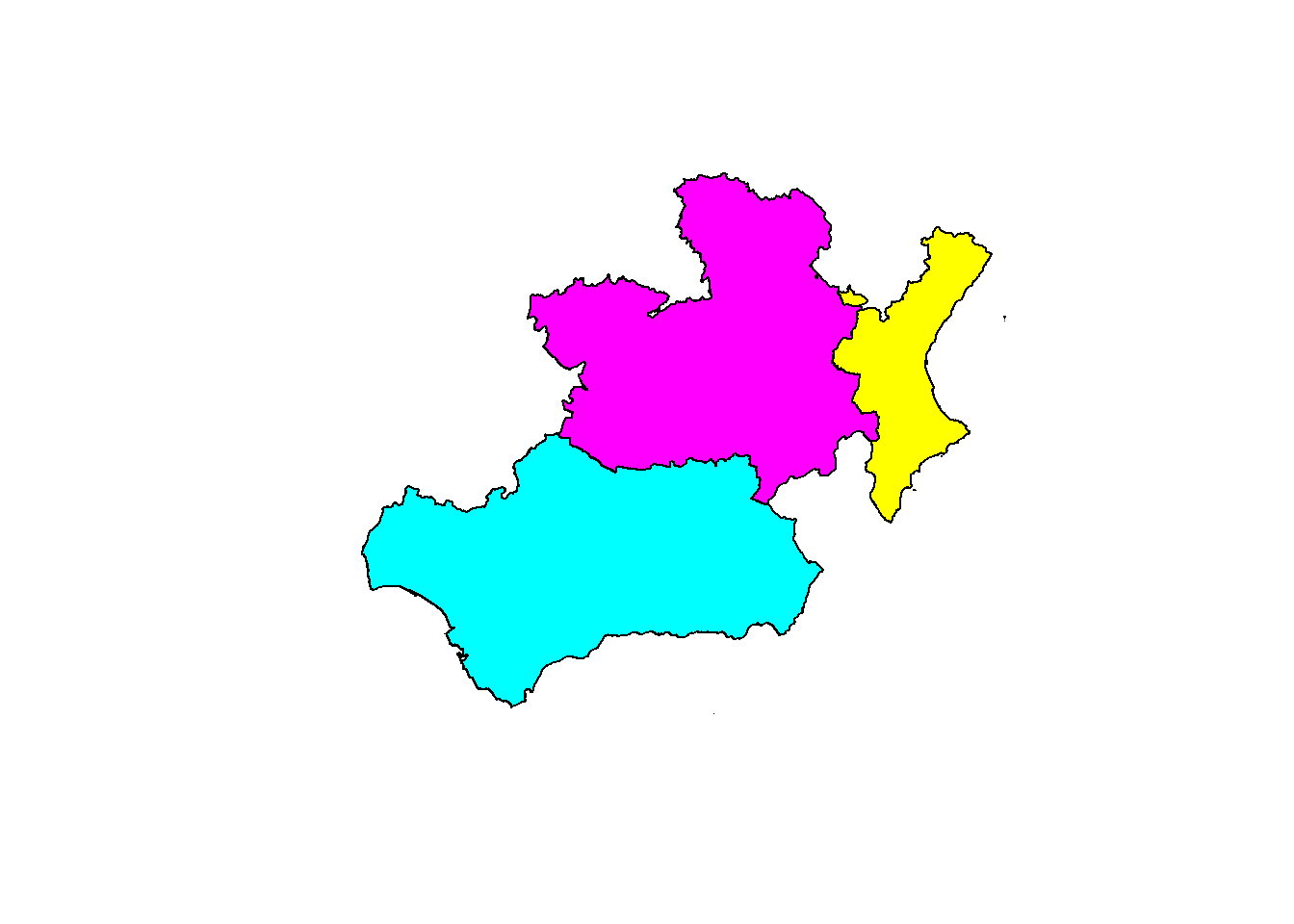
Los operadores que podemos usar para seleccionar de esta forma son entre otros:
- st_intersects(x, y, sparse = TRUE, prepared = TRUE)
- st_disjoint(x, y = x, sparse = TRUE, prepared = TRUE)
- st_touches(x, y, sparse = TRUE, prepared = TRUE)
- st_crosses(x, y, sparse = TRUE, prepared = TRUE)
- st_within(x, y, sparse = TRUE, prepared = TRUE)
- st_contains(x, y, sparse = TRUE, prepared = TRUE)
- st_contains_properly(x, y, sparse = TRUE, prepared = TRUE)
- st_overlaps(x, y, sparse = TRUE, prepared = TRUE)
- st_equals(x, y, sparse = TRUE, prepared = FALSE)
- st_covers(x, y, sparse = TRUE, prepared = TRUE)
- st_covered_by(x, y, sparse = TRUE, prepared = TRUE)
- st_equals_exact(x, y, par, sparse = TRUE, prepared = FALSE)
- st_is_within_distance(x, y, dist, sparse = TRUE)
Este tipo de funciones no devuelven geometrías sino una salida matricial lógica indicando si se cumple o no la condición. Veremos un caso concreto en contiene-intersecta.
Añadir nuevos campos a un data.frame sf
La propiedad length no da el número de objetos que contiene la colección de objetos sf. Si se trata de un objeto solo espacial, es decir que solo contiene geometrías dará length =1, pero si es una data.frame sf contendrá además de la geometría un objeto más por cada variable o columna de datos como veremos en el ejemplo:
#library(dplyr)
# creamos una data frame de puntos de 3 ciudades de españa
# además metemos el campo nombre
p_esp<- data.frame(lon=c(-3.7025599,2.1589899, -0.37739, -5.9731698),
lat= c( 40.4165001,41.3887901,39.4697495,37.3828316),
nom=c("Madrid", "Barcelona", "Valencia","Sevilla"))
# convertimos los datos a sf
p_esp <- st_as_sf(p_esp, coords = c("lon", "lat"))
# comprobamos la clase
class(p_esp)## [1] "sf" "data.frame" # pintamos los puntos
plot(st_geometry(p_esp), col="red",pch=16)
text(st_coordinates(p_esp),labels = p_esp$nom, pos=3)
#Añadimos la costa de españa
library(rworldmap)
data(countriesLow)
plot(countriesLow, add = T)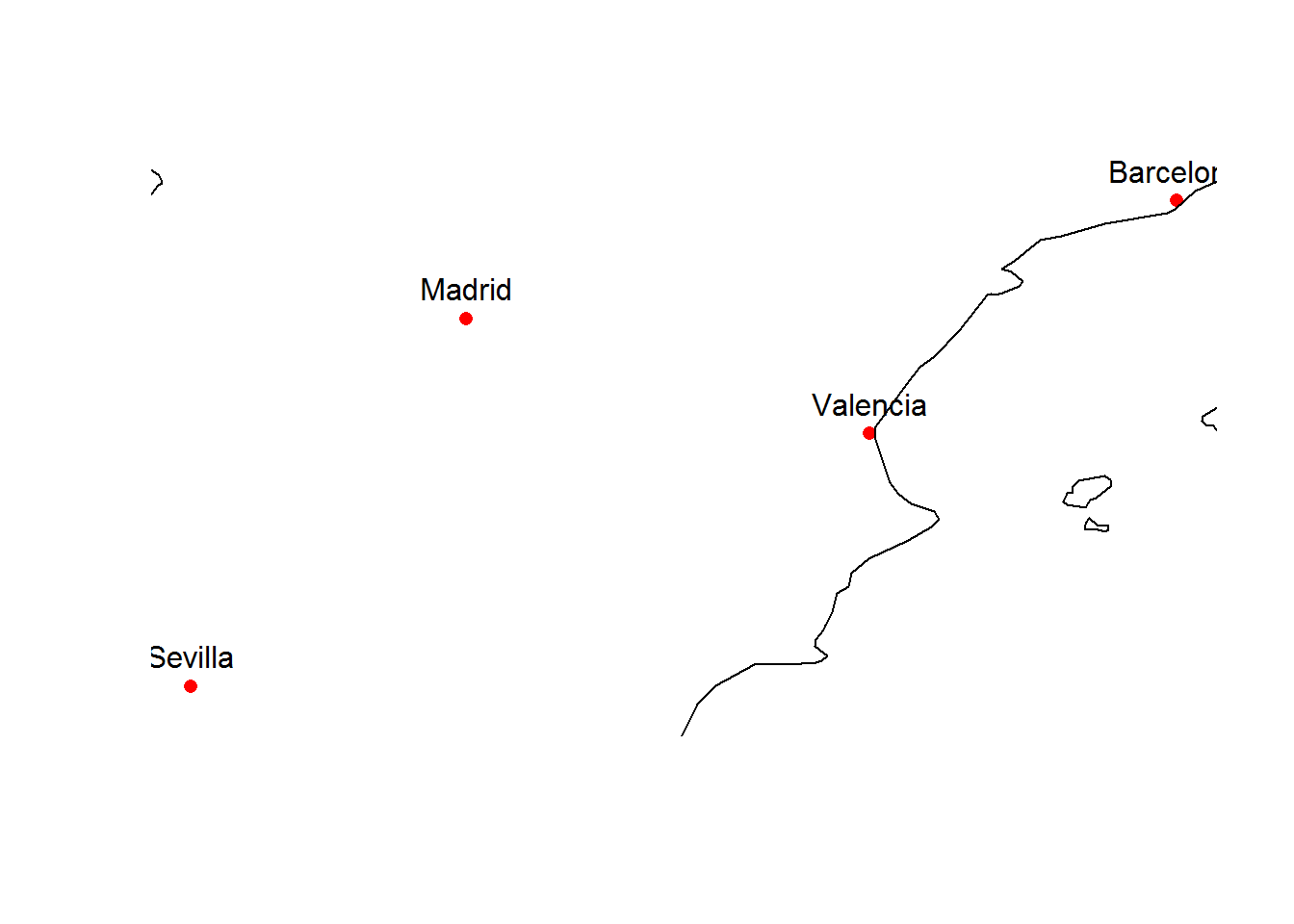
summary(p_esp)## nom geometry
## Barcelona:1 POINT :4
## Madrid :1 epsg:NA:0
## Sevilla :1
## Valencia :1 length(p_esp)## [1] 2 # Añadimos un nueva columan de datos
p_esp$habitantes<-c(3.2,1.62,0.79,0.70)
# pintamos de nuevo
plot(st_geometry(p_esp), col="red",pch=16)
text(st_coordinates(p_esp),
labels = paste(p_esp$nom, "\n","hab:", p_esp$habitantes),
pos=3)
plot(countriesLow, add = T)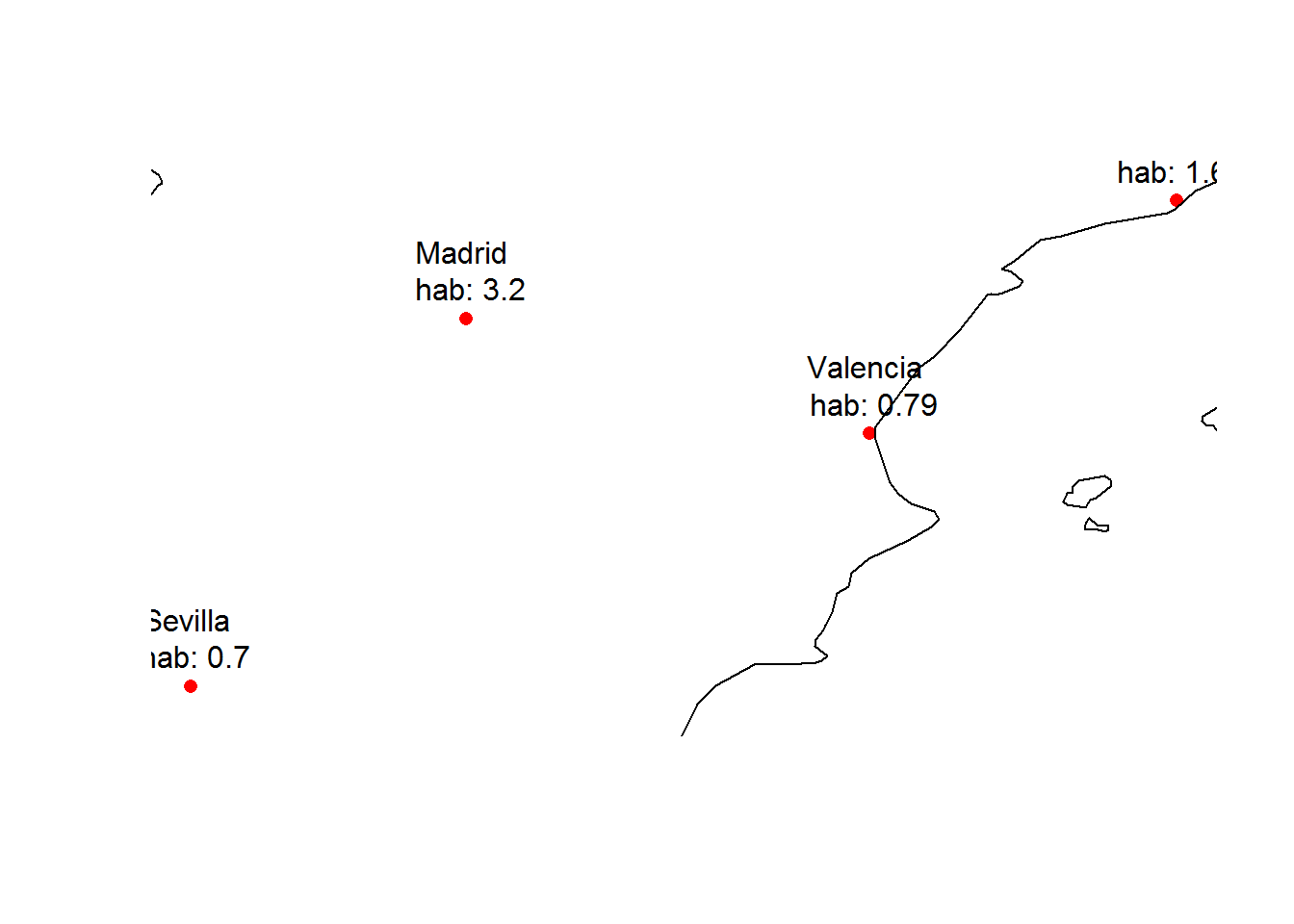
Conversión
simplify
Las capas con geometrías ocupan mucho espacio en disco y R trabaja todo en memoria, por eso el comando simplify es muy interesante. Permite reducir el tamaño de la geometría, simplificando trazos. Aunque cambia respecto a la original, por lo que en ciertos casos hay que usarlo con cuidado.
Veamos por ejemplo el caso de la capa de autonomías de España.
# Medir el tamaño del archivo de cc autónomas
pryr::object_size(autonomias)## 13 MB # Calcular el numero de puntos totales de la capa
pts_autonomias <- st_cast(autonomias$geometry, "MULTIPOINT")
cnt_autonomias <- sapply(pts_autonomias, length)
sum(cnt_autonomias)## [1] 1486814 # hacemos lo mismo con una nueva capa reducida
# Simplify object reducir vertices
autonomias_simple <- st_simplify(autonomias,
preserveTopology = T,
dTolerance = 0.05)
# tamaño en megas del objeto
pryr::object_size(autonomias_simple)## 1.68 MB # numero de puntos
pts_autonomias_simple <- st_cast(autonomias_simple$geometry, "MULTIPOINT")
cnt_autonomias_simple <- sapply(pts_autonomias_simple, length)
sum(cnt_autonomias_simple)## [1] 38762sp a sf
Para los que siguen trabajando con la librería sp, la forma de convertir de uno a otro tipo es así:
rios <- st_read("capas/Cauces - Nivel 0.shp")
class(rios)
# Convertir a Spatial object
rios_sp <- as(rios, Class = "Spatial")
class(rios_sp)dataframe a sf
De tabla con datos lon-lat o x-y a objeto sf. El proceso es crear la geometría, añadir el sistema de referencia, con la función st_as_sf()
require(sf)
# Simple dataframe
pts <- data.frame(ID = 1:2, lon = c(-2, 1),lat = c(41, 42))
# pintamos los puntos
# plot(st_geometry(autonomias), col = "grey")
# points(pts$lon,pts$lat,col="red",pch = 19)
# Convertimos de data.frame de puntos a sf
pts1 <- st_as_sf(pts, coords = c("lon", "lat"))
# el sistema CRS por defecto es NA
st_crs(pts1)## Coordinate Reference System: NA # para crear un sf con crs distinto de NA hacemos:
# donde crs= codigo epsg
pts2<-st_as_sf(pts, coords = c("lon", "lat"), crs = 2062)
st_crs(pts2)## Coordinate Reference System:
## EPSG: 2062
## proj4string: "+proj=lcc +lat_1=40 +lat_0=40 +lon_0=0 +k_0=0.9988085293 +x_0=600000 +y_0=600000 +a=6378298.3 +b=6356657.142669561 +pm=madrid +units=m +no_defs"puntos xy a sf
Simplemente pasamos los puntos a un data frame y procedemos como antes.
Necesitamos la función st_as_sf() indicando si los datos son x-y o lon-lat o el nombre de los campos o columnas que sea la x y la y en un vector y el crs de la capa si lo conocemos.
El CRS puede ser especificado como proj4 o EPSG. Ejemplo:c_sf <- st_as_sf(tablaxy, coords = c("nombre_campo_X","nombre_campo_Y"), crs = 4326)
# creamos una data frame de puntos de 3 ciudades de españa
# además metemos el campo nombre
p_esp<- data.frame(lon=c(-3.7025599,2.1589899, -0.37739, -5.9731698),
lat= c( 40.4165001,41.3887901,39.4697495,37.3828316),
nom=c("Madrid", "Barcelona", "Valencia","Sevilla"))
# convertimos los datos a sf
p_esp <- st_as_sf(p_esp, coords = c("lon", "lat"))
# comprobamos la clase
class(p_esp)## [1] "sf" "data.frame" # pintamos los puntos
plot(st_geometry(p_esp), col="red",pch=16)
text(st_coordinates(p_esp),labels = p_esp$nom, pos=3)
sf a fichero x-y
Ver también apartado de escritura.
Para extraer las coordenadas de una capa en formato de tabla y escribirla en un fichero usaremos el comando st_write(), pero hay que usar un comando oculto para que realmente escriba las coordenadas esplicitamente con layer_options = "GEOMETRY=AS_XY".
# sacar las coordenadas de una capa a un fichero csv
st_write(pts2, "pts.csv", layer_options = "GEOMETRY=AS_XY")sf a geometría
Los objetos sf contienen tablas de datos y muchas veces al representarlos con plot nos dibuja un mapa para cada variable del data frame asociado. Por esto necesitaremos indicar que queremos que pinte solo la geometría del objeto con la función st_geometry().
# comprobamos que la dimension de campos de la capa
length(autonomias_simple) # son 4 -1 de geometría 3## [1] 4 # si pintamos nos dibuja cada campo
plot(autonomias_simple)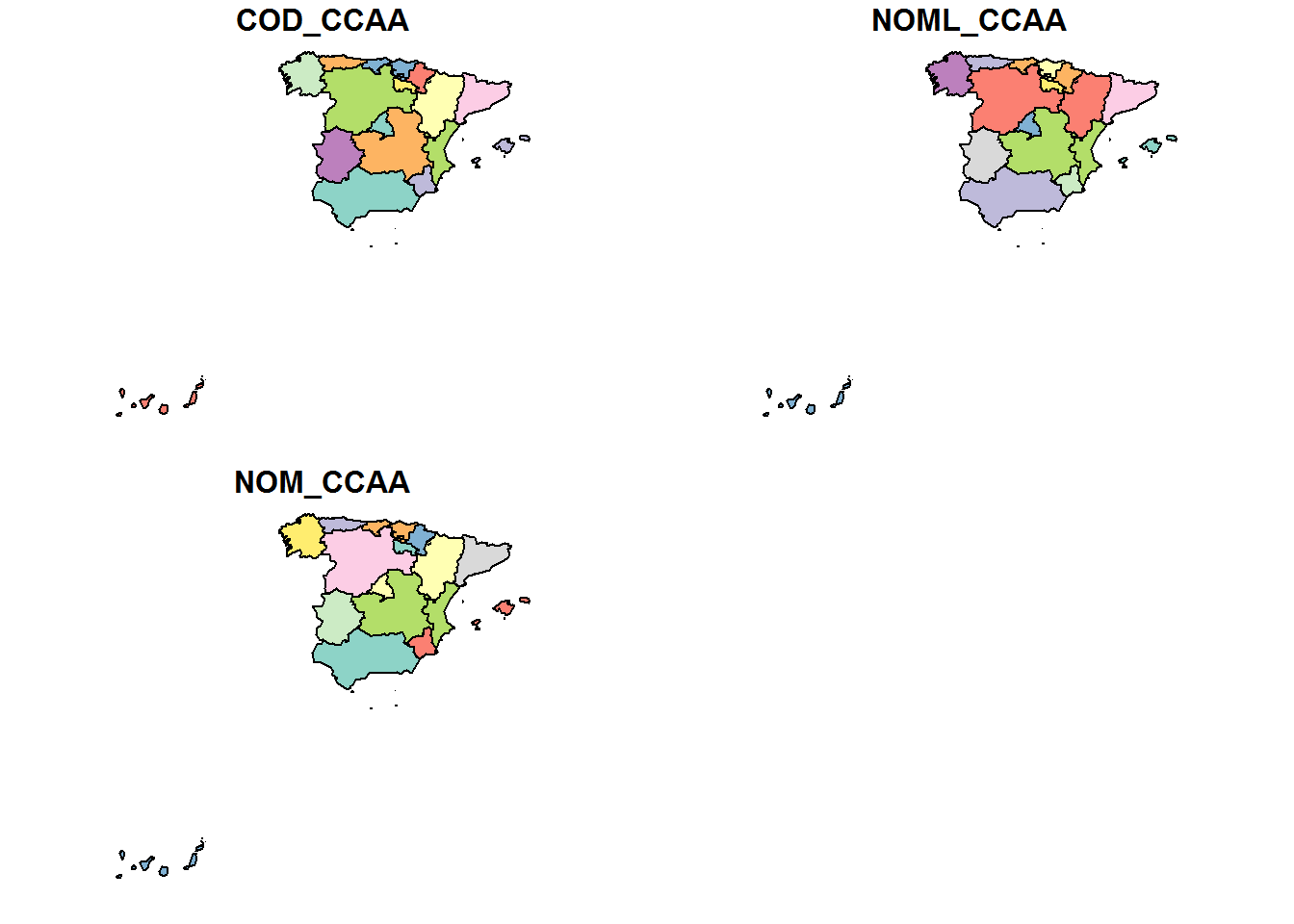
# si queremos solo la geometría hacemos esto
plot(st_geometry(autonomias_simple),col=1:19)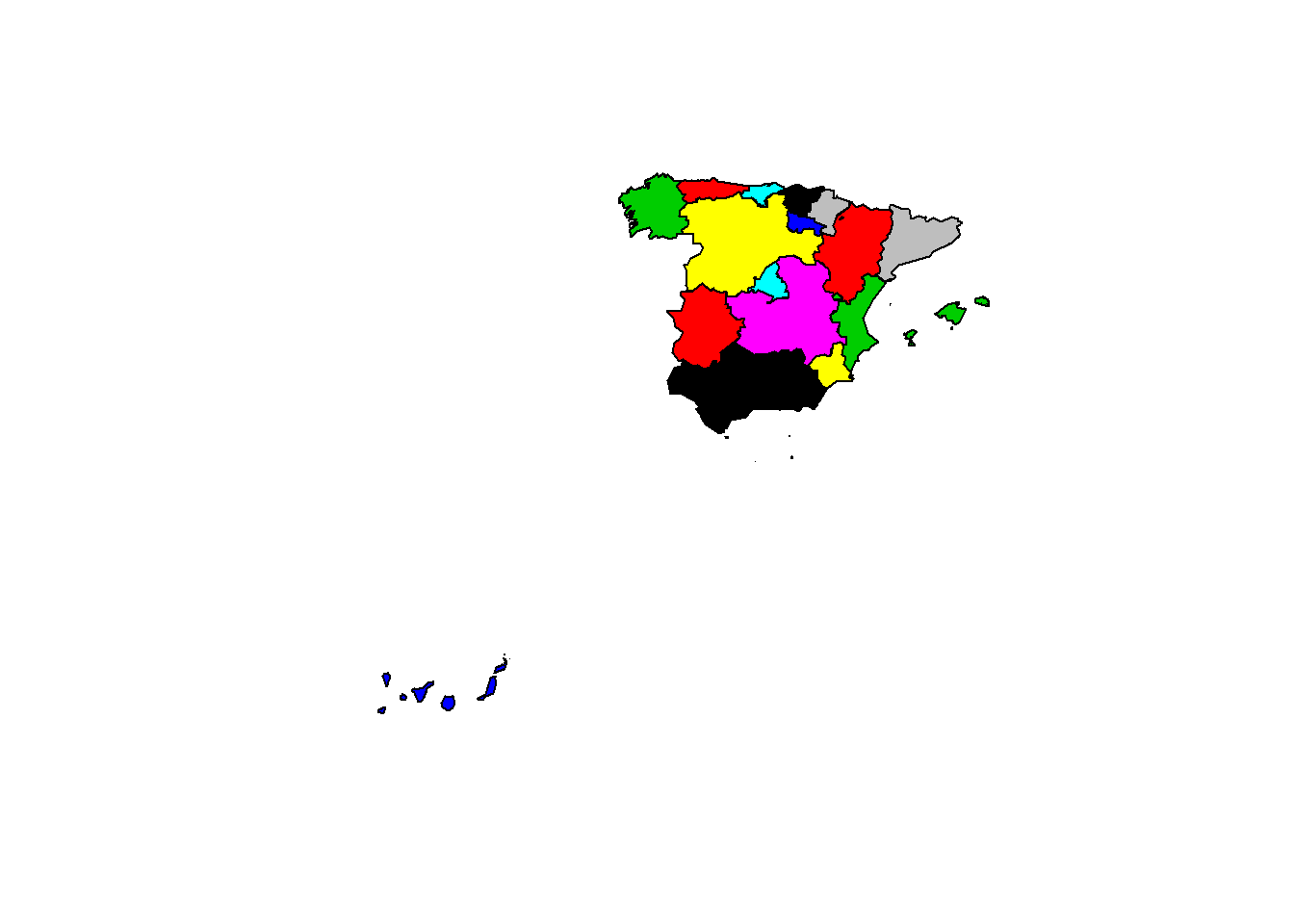
geometría a sf {##geometria-a-sf}
El caso contrario es cuando tenemos solo una capa de geometría, pero que no tiene ninguna tabla de datos asociada.
Asignar un nuevo campo de tabla es muy sencillo, pero lo habitual es usar la función st_sf(). Veamos un ejemplo:
# creamos una data frame de puntos de 3 ciudades de españa
ciudades<- data.frame(lon=c(-3.7025599,2.1589899, -0.37739, -5.9731698),
lat= c( 40.4165001,41.3887901,39.4697495,37.3828316))
# convertimos los datos a sf
ciudades <- st_as_sf(ciudades, coords = c("lon", "lat"))
class(ciudades)## [1] "sf" "data.frame" ciudades_geo<-st_geometry(ciudades)
class(ciudades_geo)## [1] "sfc_POINT" "sfc" length(ciudades_geo)## [1] 4 # transformamos en sf la geometría
ciudades2<-st_sf(ciudades_geo)
class(ciudades2)## [1] "sf" "data.frame" ciudades2$nom=c("Madrid", "Barcelona", "Valencia","Sevilla") Como vemos la capa ciudades_geo es del tipo sfc, que indica que es una colección de objetos geométricos, pero no un sf. Sin embargo la capa ciudades2, si es un sf, y además le asignamos un campo como si se tratara de una data.frame.
Operaciones espaciales
Desplazamiento y giro
Estas transformaciones simples se suelen denominar operaciones afines y se trata simplemente de desplazamientos y giros de capas espeaciales.
Vamos a realizar unas transformaciones afines simples a la capa del límite de la CCAA de Madrid simplificado en coordenadas UTM.
Haremos un desplazamiento en eje X y otro en Y. Para el giro tenemos que hace una función simple llamada rot que transforma las coordenadas. Las unidades UTM son en metros. En la transformación de giro necesitamos definir un punto de giro, que será el centroide de la capa, y además le aplicamos una escalación multiplicando por 0.5.
##Obtener el limite de la CAM
# Selecciono una CCAA de la capa autonomías de ejemplo
madrid<-autonomias[autonomias$NOM_CCAA == "MADRID",]
# la simplifico para que ocupe menos
madrid<-st_simplify(madrid,
preserveTopology = T,
dTolerance = 0.02)
# como tienen varios poligonos he decidido quedarme solo con el principal
# para eso transforomo en lineas y me quedo con el principal que es el 2
madrid<-st_transform(madrid,crs=23030)
madrid<-st_geometry(madrid)
m1<-st_cast(madrid,"LINESTRING") # transformo a lineas
# veo con length(m1)=3 que hay 3 poligonos linea principales
madrid<-m1[2] # me quedo con el 2 que mas grande y quito las islas
madrid<-st_cast(madrid,"POLYGON") # transformo a poligono de nuevo
# Realizamos las transformaciones afines sobre esa capa
# Desplazamiento en eje x e y
mx<- madrid + c(6000,0)
my<- madrid + c(0,10000)
# Giro
rot = function(a) matrix(c(cos(a), sin(a), -sin(a), cos(a)), 2, 2)
#Centro de giro
m_centro<-st_centroid(madrid)
# aplicamos giro y escala por 0.5
m_giro90 = (st_geometry(madrid) - m_centro) * rot(pi/2) *0.5 + m_centro
plot(madrid, col="grey")
plot(mx,border="red",lty=2,add=T)
plot(my,border="blue",add=T)
plot(m_giro90,col="purple",lwd=2, lty=3,add=T)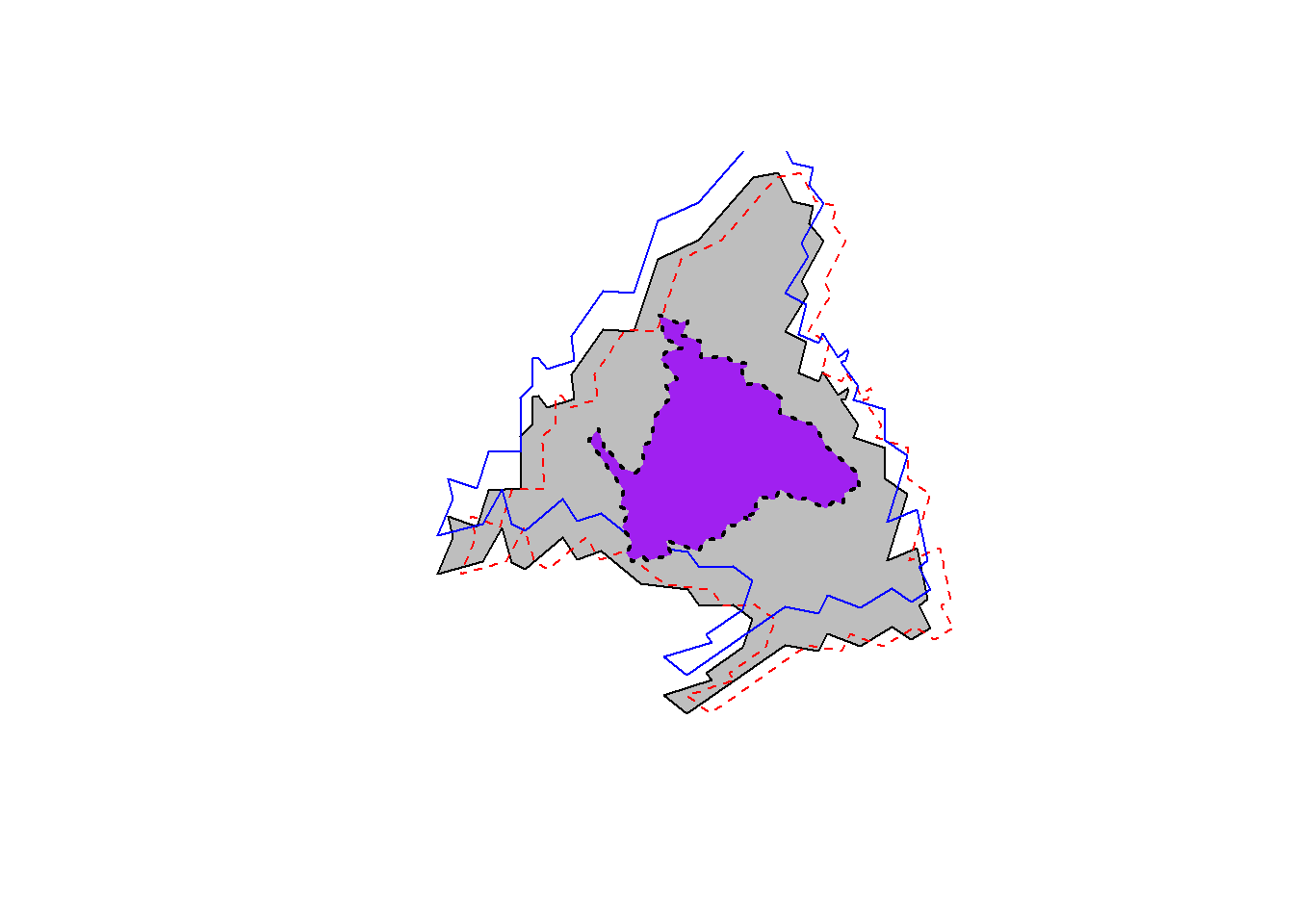
Buffer
El bufer es el polígono que encierra el resultante de dar una determinada distancia en torno a un punto, línea o polígono. Se utiliza mucho para procesos de análisis espacial y la librería sf contienen una función simple para hacerlos st_buffer(geometria, dist=).
La distancia es la separación que hacemos desde la linea de la capa origen, pero hemos de tener en cuenta que las unidades son las de la capa.
En este ejemplo vamos a trabajar con el límite de la comunidad autónoma de Madrid y vamos a pintar un buffer exterior y otro interior. La capa está en UTM por lo que la distancia es en metros.
# par(bg=gray(1),oma=c(0.1,0.1,0.1,0.1),mar=c(0.1,0.1,0.1,0.1))
# Calculo 2 capas de buffer una exterior y otra interior
mad_buf1<-st_buffer(st_geometry(madrid), dist = 2000)
mad_buf2<-st_buffer(st_geometry(madrid), dist = -5000)
# pinto las capas
plot(st_geometry(madrid),lwd=2)
plot(st_geometry(mad_buf1),border="red",add=T)
plot(st_geometry(mad_buf2),border="blue",add=T)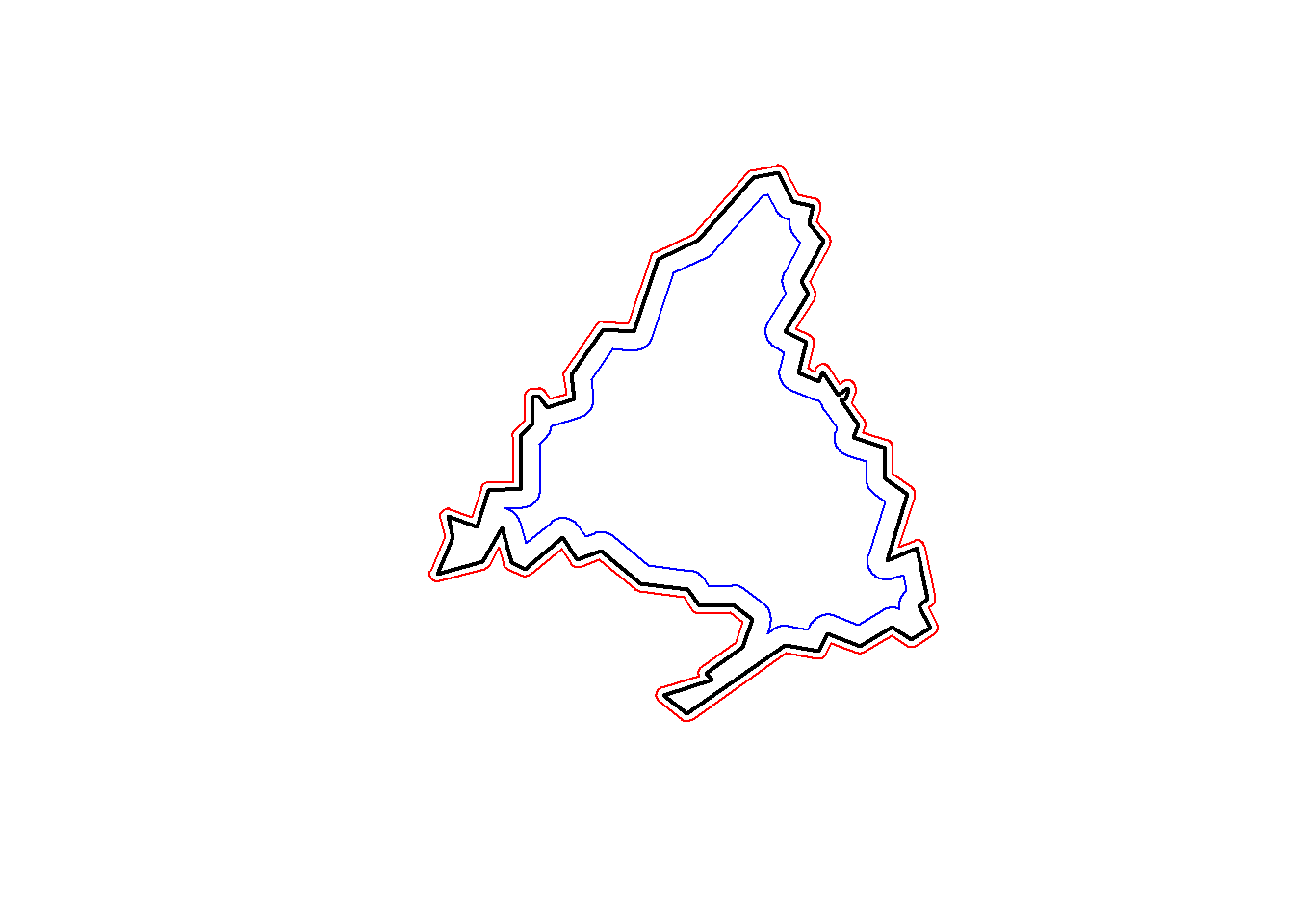
Centroide
El centroide es el baricentro o centro de masas de una geometría. En el caso de multipolígonos la función st_centroid(), nos permite seleccionar la opción de dar el centro de masas total o el del elemento mayor (con el argumento of_largest_polygon = TRUE).
# selecciona aragón
aragon<-autonomias[autonomias$NOM_CCAA == "ARAGON",]
plot(st_geometry(aragon),col=gray(0.4))
plot(st_centroid(aragon),add=T, pch = 1, cex=2)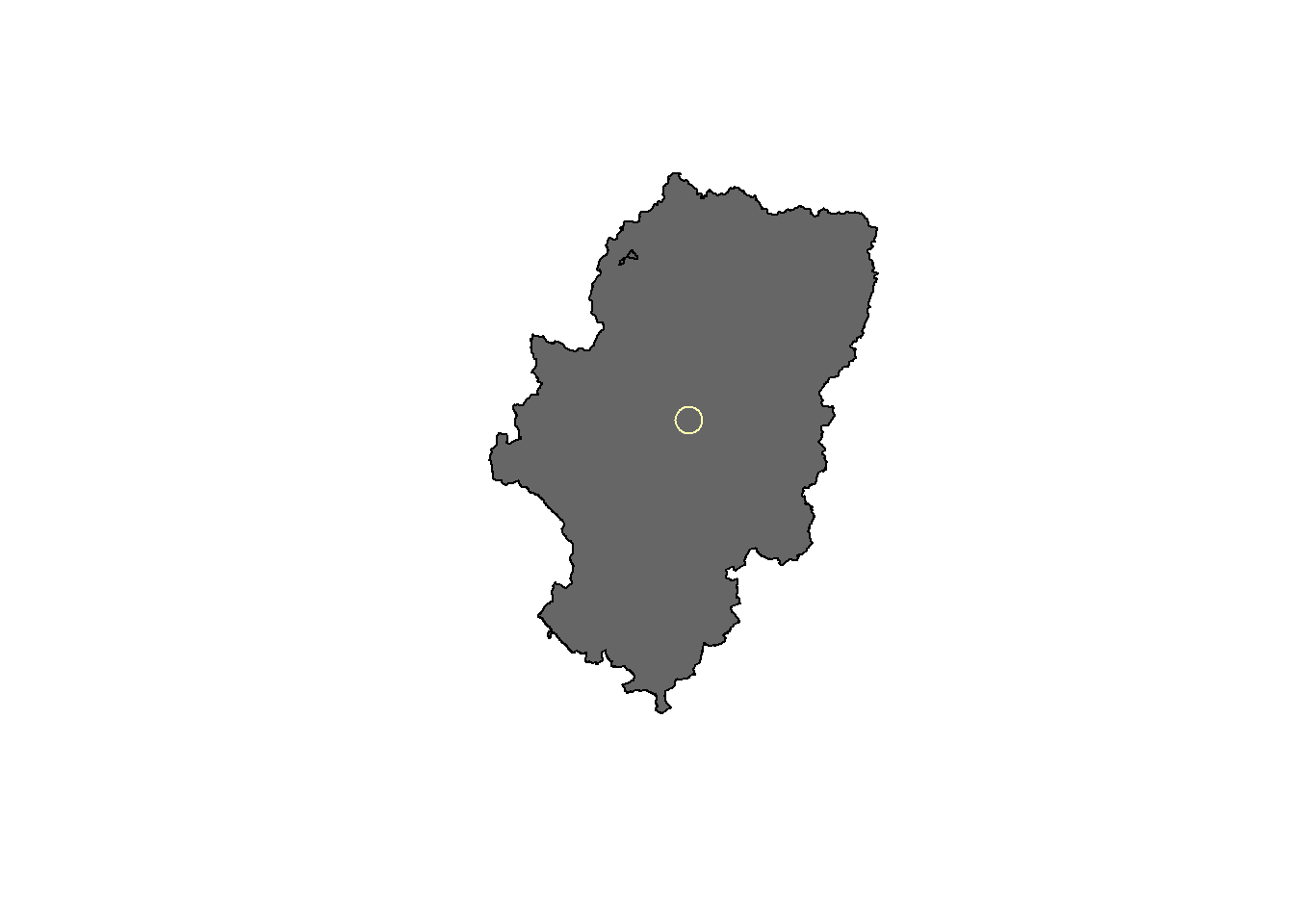
# # pinto las que tocan a aragón
# toca_aragon<-autonomias[aragon, op = st_touches]
# plot(st_geometry(toca_aragon),col=gray(0.4))
# plot(st_geometry(aragon),col=gray(0.7), add=T)
#autonomias %>% filter(lengths(st_touches(., aragon)) > 0)bbox caja
Esta operación consiste en seleccionar una caja o rectángulo que englobe y contenga una capa. La función habitual es st_bbox(capa) que nos proporciona el rectángulo en el que se inscribe la capa, pero lo mas habitual es que queramos un polígono de este rectángulo y no solo las coordenadas de los vértices y esto lo hacemos con grid.
# caja alrededdor de aragon
caja_aragon <- st_make_grid(aragon, n = 1)
# datos de la caja que envuelve la capa
st_bbox(aragon)## xmin ymin xmax ymax
## -2.1736713 39.8467782 0.7713067 42.9244952 # pintamos las capas
plot(st_geometry(aragon),col=gray(0.4))
plot(st_geometry(caja_aragon),add=T)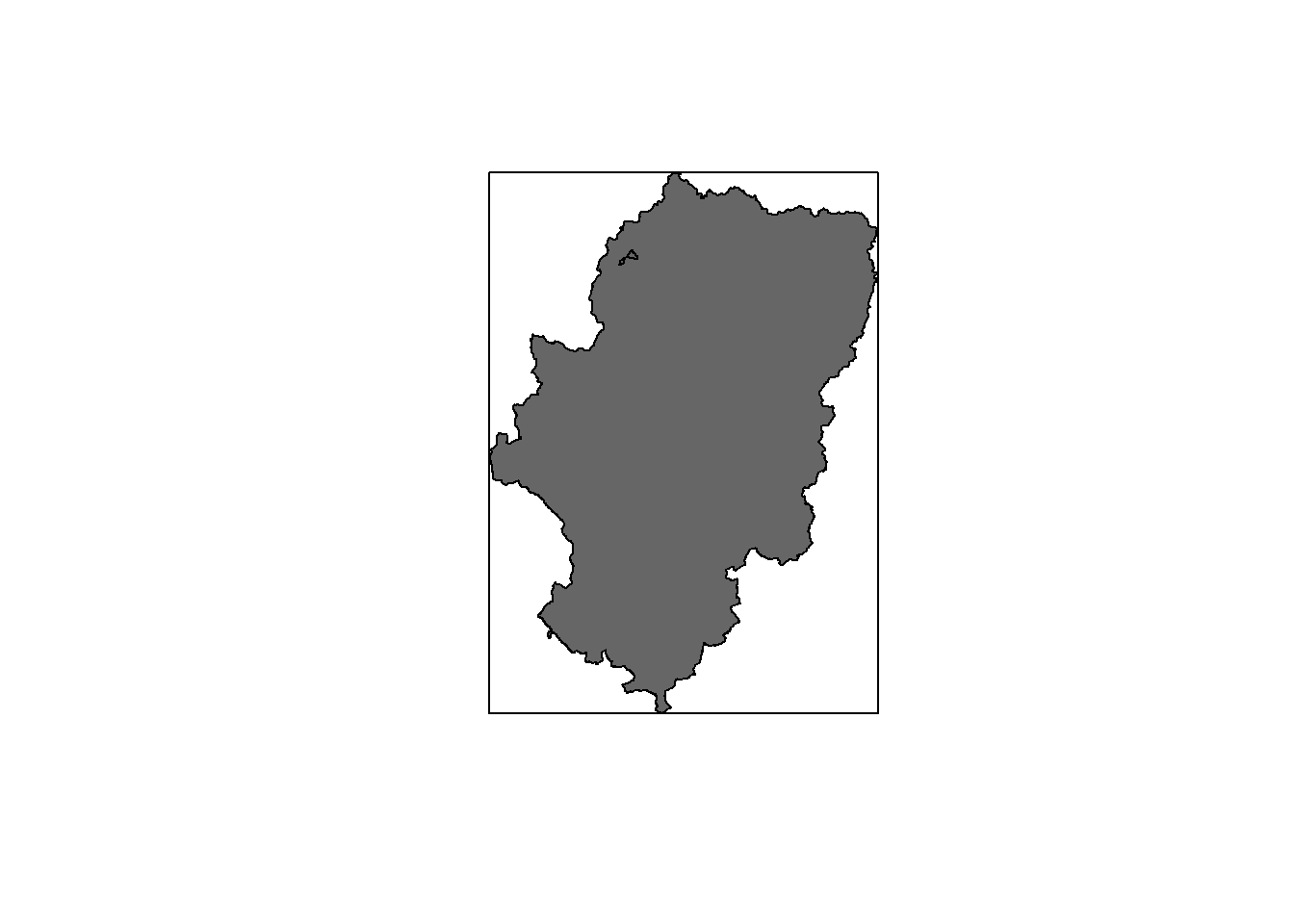
plot(st_geometry(aragon),col=gray(0.3))
plot(st_geometry(st_make_grid(aragon, n = 4)),add=T)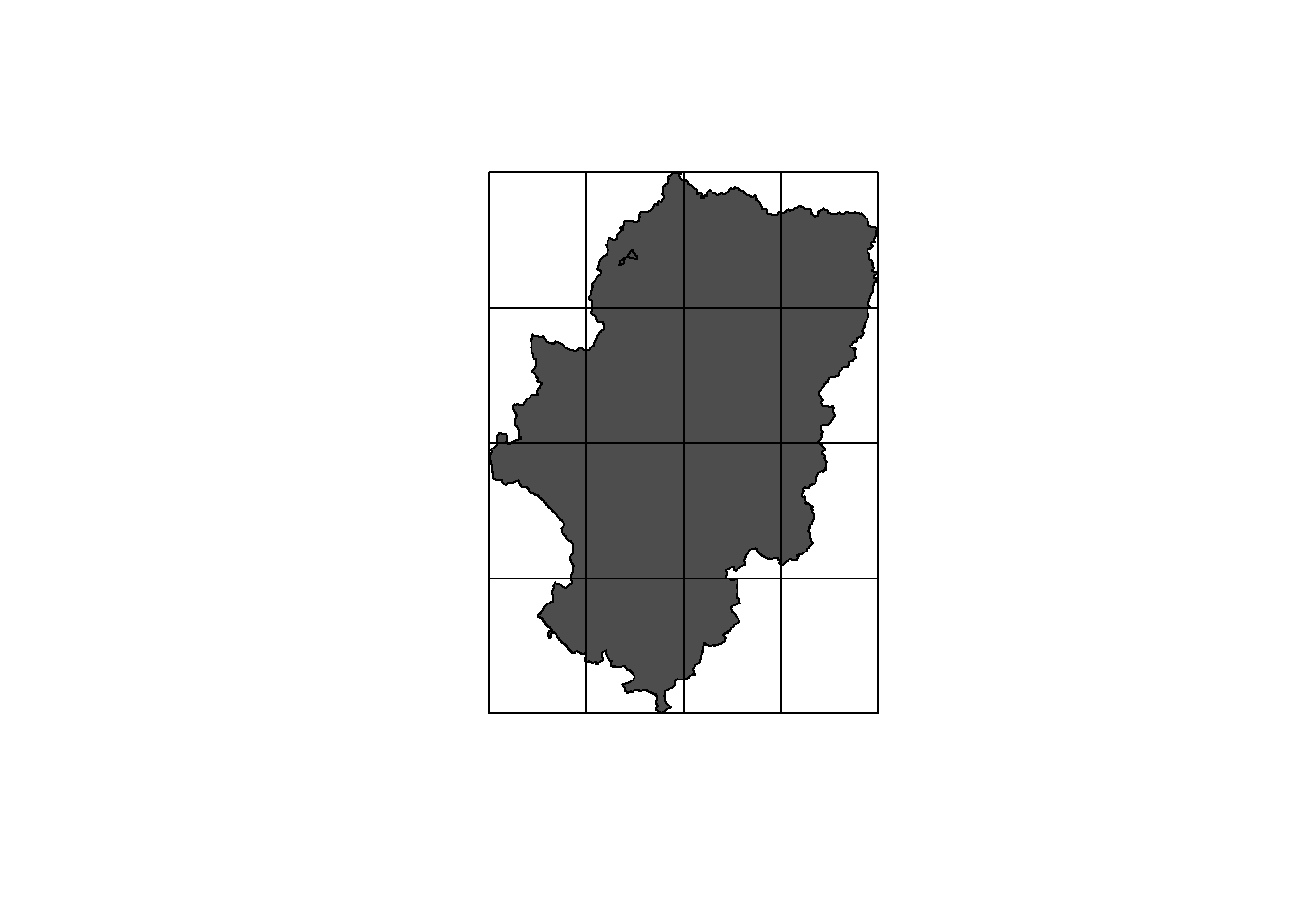
Unir capas
Hay que comprender como son los objetos sf antes de unirlos, pues en algunas ocasiones podemos hacer un lío sin querer. Las uniones no se pueden hacer sobre objetos simples como POINTS pues trata cada uno como una capa nueva, hay primero que unir la propia capa y transformarla en MULTIPOINT para unirla con otra.
Unir puntos
La precaución que hay que tener es que NO se pueden unir capas de tipo POINT, y solo debemos hacerlo con MULTIPOINTS.
En el siguiente ejemplo veremos la diferencia entre unir POINTS y MULTIPOINTS. Creamos dos capas aleatorias de 10 puntos cada una y las unimos con st_union. Como veremos, al crear las capas con un data frame, se forma una capa de 10 POINT, si unimos esta capa a otra de 10 POINT nos genera una de 100 POINT. Sin embargo si antes de unir las capas transformamos cada una en MULTIPOINT usando st_union en cada capa, la unión final es una capa de 10+10 =20 puntos.
# creamos un data frame aleatorio xy entre 0 y 1000
xy<-data.frame(id=1:10,x=runif(10)*1000,y=runif(10)*1000)
#Repetimos para crear la capa 2
xy2<-data.frame(id=101:110,x=runif(10)*1000,y=runif(10)*1000)
# comvertimos a sf y unimos para crear un multipoint por capa
xy_sf <- st_union(st_as_sf(xy, coords = c("x", "y"), crs=25831))
xy2_sf <- st_union(st_as_sf(xy2, coords = c("x", "y"), crs=25831))
# representamos los puntos
plot(st_geometry(xy_sf), col="blue",pch = 19)
plot(st_geometry(xy2_sf), col="red",pch = 19,add=T)
# comprobamos que es MULTIPOINT
class(xy_sf)## [1] "sfc_MULTIPOINT" "sfc" # Unimos las 2 capas de multipoints
xy_b_union<-st_union(xy_sf,xy2_sf)
class(xy_b_union)## [1] "sfc_MULTIPOINT" "sfc" # comprobamos que son 20 puntos
length(st_cast(xy_b_union,"POINT"))## [1] 20 #length(xy_b_union)
plot(st_geometry(xy_b_union), col="red" ,pch = 19)
Unir polígonos
Con los polígonos, st_union() disolverá todos los polígonos en un solo polígono que representa el área superpuesta de todos.
# creamos una capa de puntos
d = data.frame(matrix(runif(15), ncol = 3))
names(d)<-c("x", "y", "z")
d$z<-d$z*10
puntos = st_as_sf(x = d, coords = 1:2)
# creamos una capa de poligonos con buffer sobre los puntos
# Buffer de capa de puntos
p_buffer <- st_buffer(puntos, dist=0.3)
# Limitamos a solo la geometry
p_buffers <- st_geometry(p_buffer)
# numero de geometrías en la capa
length(p_buffers)## [1] 5 # dimension de estas geometrias 2=superficie
st_dimension(p_buffers)## [1] 2 2 2 2 2 # Plot
plot(p_buffers,col=1:5)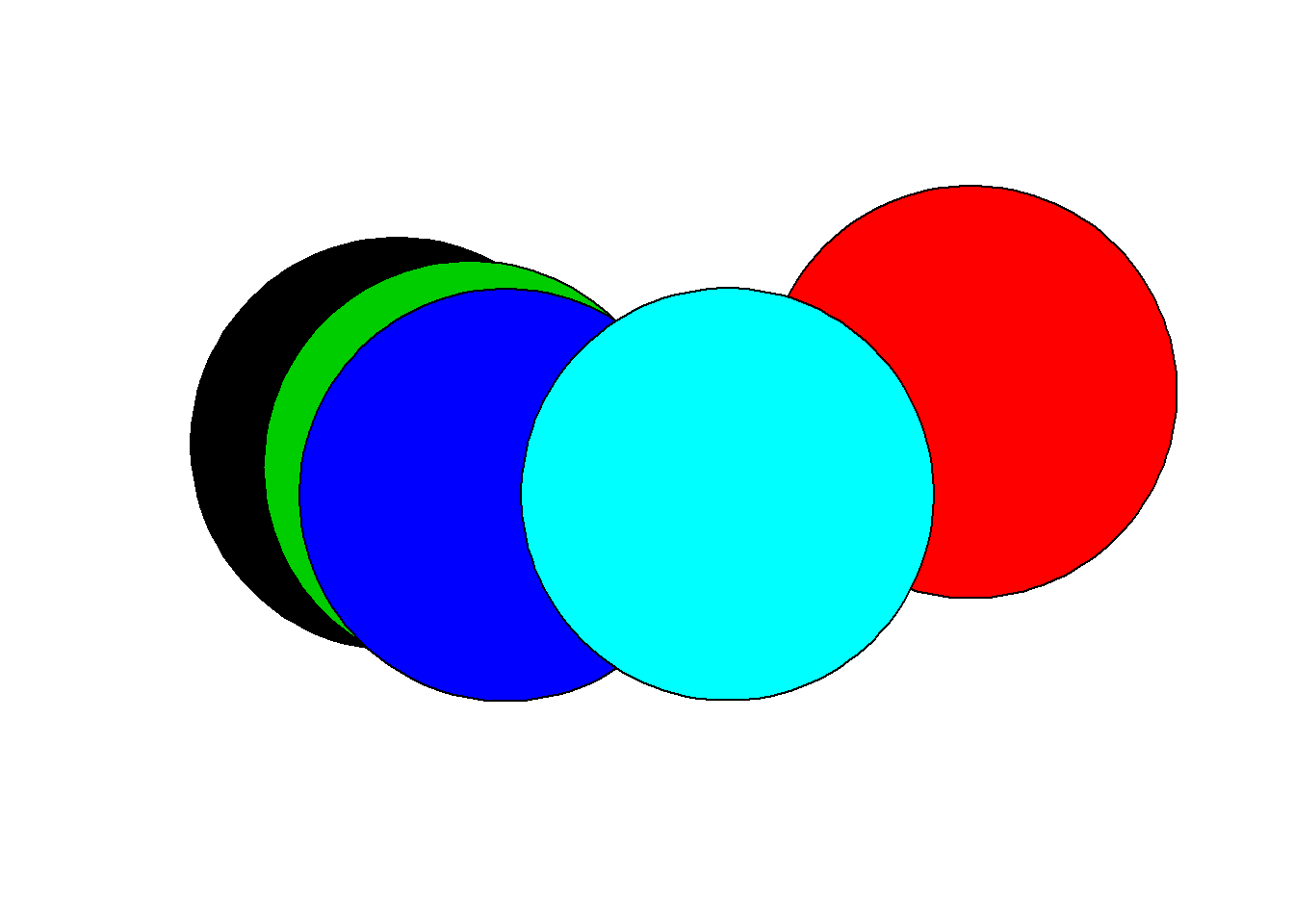
# unimos la geometria
p_buf_union <- st_union(p_buffers)
# numero de geometrías en la capa unida
length(p_buf_union)## [1] 1 # Plot
plot(p_buf_union)
Asignar datos por geometría aggregate
Si tenemos una capa de puntos y otra de polígonos, y queremos calcular la media de los valores de puntos en cada polígono usaremos aggregate.
Queremos asignar a cada polígono la media de los valores que da la capa de puntos que caen dentro de cada polígono. Veamos un ejemplo
# generamos un poligono formado por otros 2
# resultado de dividir un cuadrado por la diagonal
m1 = cbind(c(0, 0, 1, 0), c(0, 1, 1, 0))
m2 = cbind(c(0, 1, 1, 0), c(0, 0, 1, 0))
# transformamos en una lista sf los 2 pol
pol = st_sfc(st_polygon(list(m1)), st_polygon(list(m2)))
plot(pol,col=1:2)
class(pol)## [1] "sfc_POLYGON" "sfc" str(pol)## sfc_POLYGON of length 2; first list element: List of 1
## $ : num [1:4, 1:2] 0 0 1 0 0 1 1 0
## - attr(*, "class")= chr [1:3] "XY" "POLYGON" "sfg" # vamos a generar una capa de puntos aleatoria
set.seed(1988)
d = data.frame(matrix(runif(15), ncol = 3))
names(d)<-c("x", "y", "z")
d$z<-d$z*10
puntos = st_as_sf(x = d, coords = 1:2)
plot(pol)
plot(puntos,pch = 5,lwd=5, add = TRUE)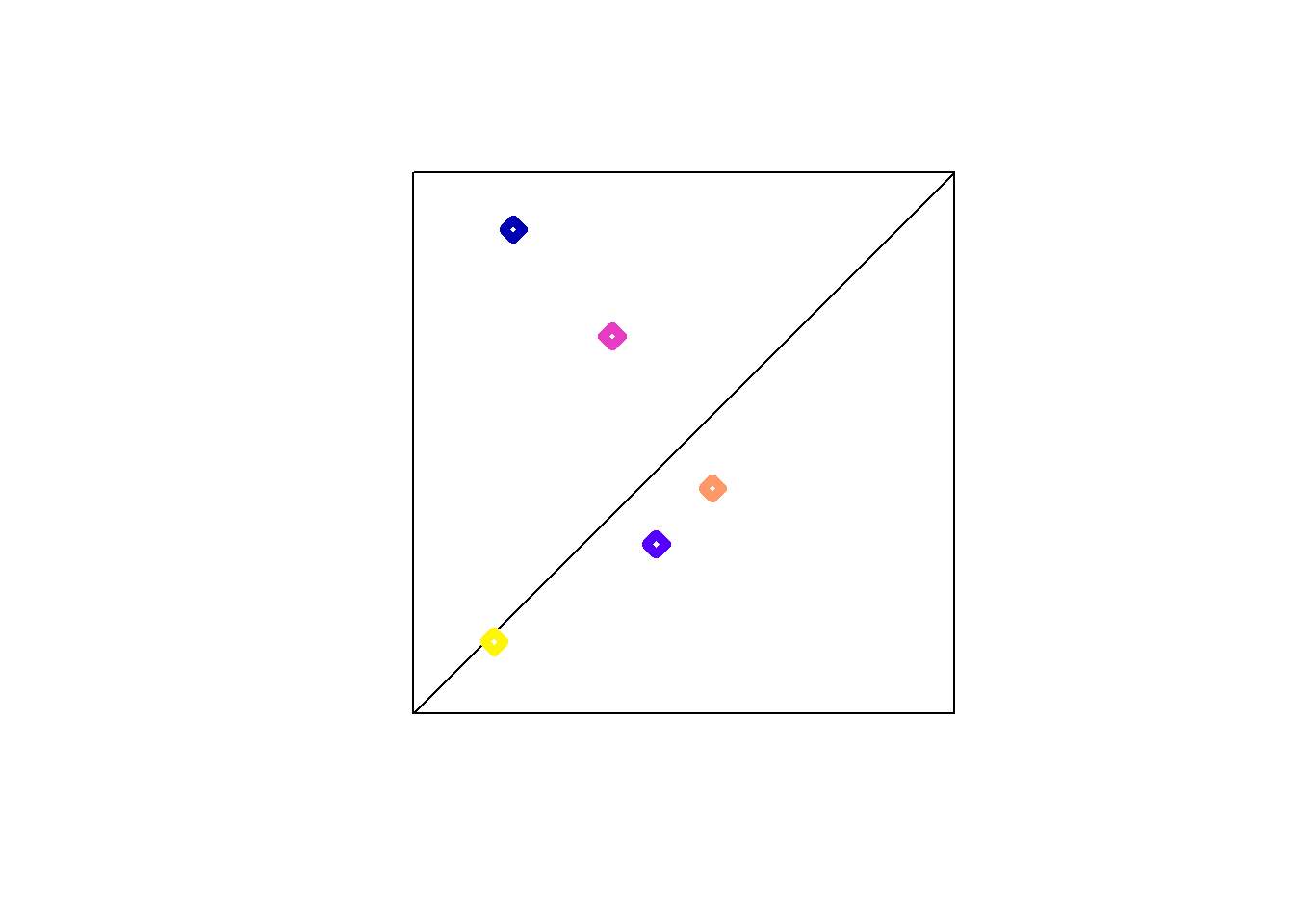
# Usamos aggregate
# calculamos la media en cada poligono
p_ag1 = aggregate(puntos, pol, mean)
plot(p_ag1)
plot(puntos,pch = 5,lwd=5, add = TRUE)
text(d$x, d$y, labels=round(d$z,2), cex= 0.8, pos=3)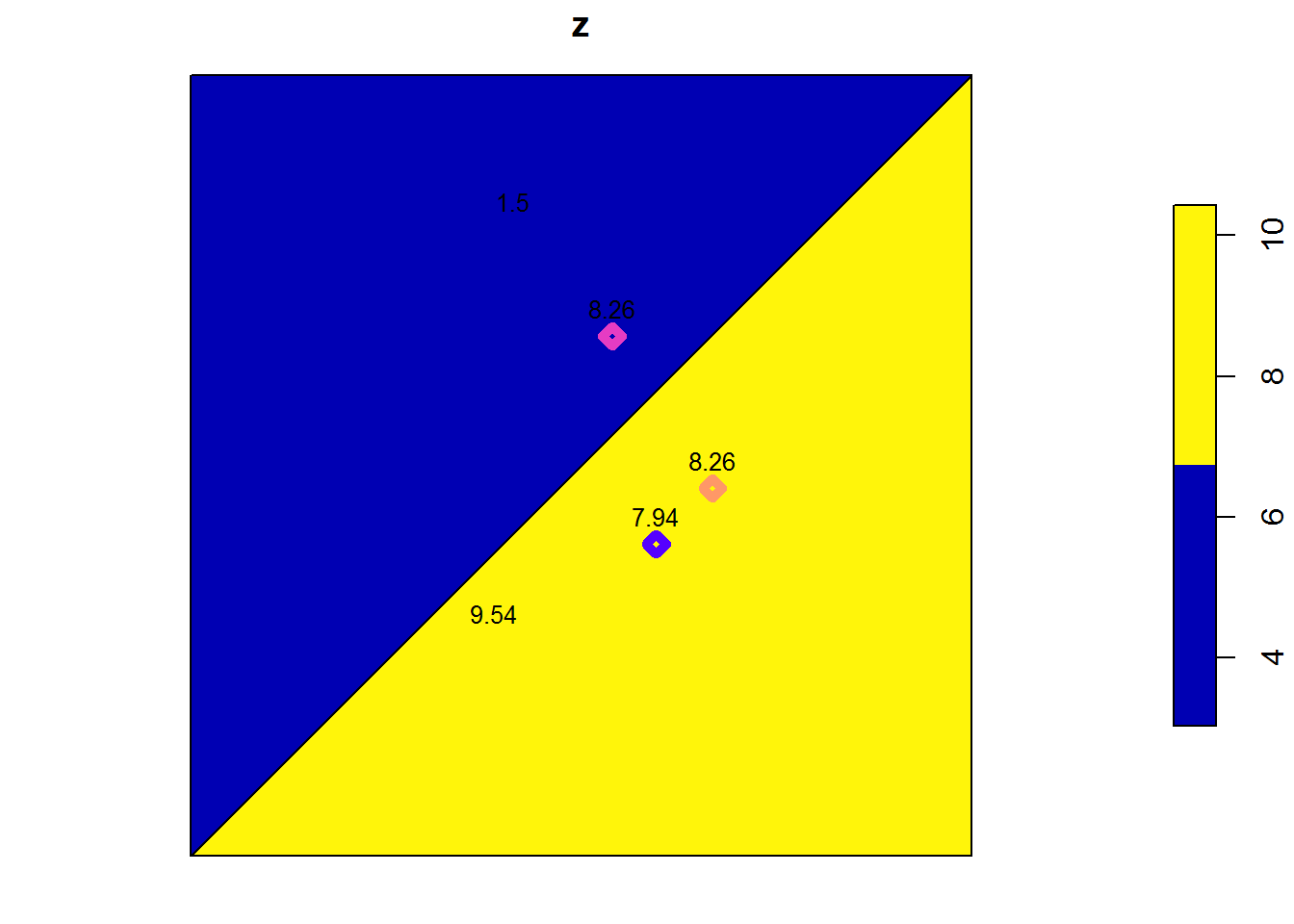
st_dimension(p_ag1)## [1] 2 2Envolvente convexa
La envolvente convexa de una capa de puntos es el polígono de superficie mínima que contiene a todos los puntos, y cuyos vértices son también algunos de los puntos.
La función st_convex_hull() calcula la envolvente dado una capa MULTIPOINT, es decir si son POINT antes tendremos que hacer un st_union() para combinarlos.
plot(xy_b_union)
# como es ya una capa MULTIPOINT nos da uno el numero de geometrías
length(xy_b_union)## [1] 1 puntos_hull <- st_convex_hull(xy_b_union)
# Plot the points together with the hull
plot(st_geometry(xy_b_union), col = "red")
plot(puntos_hull, add = T)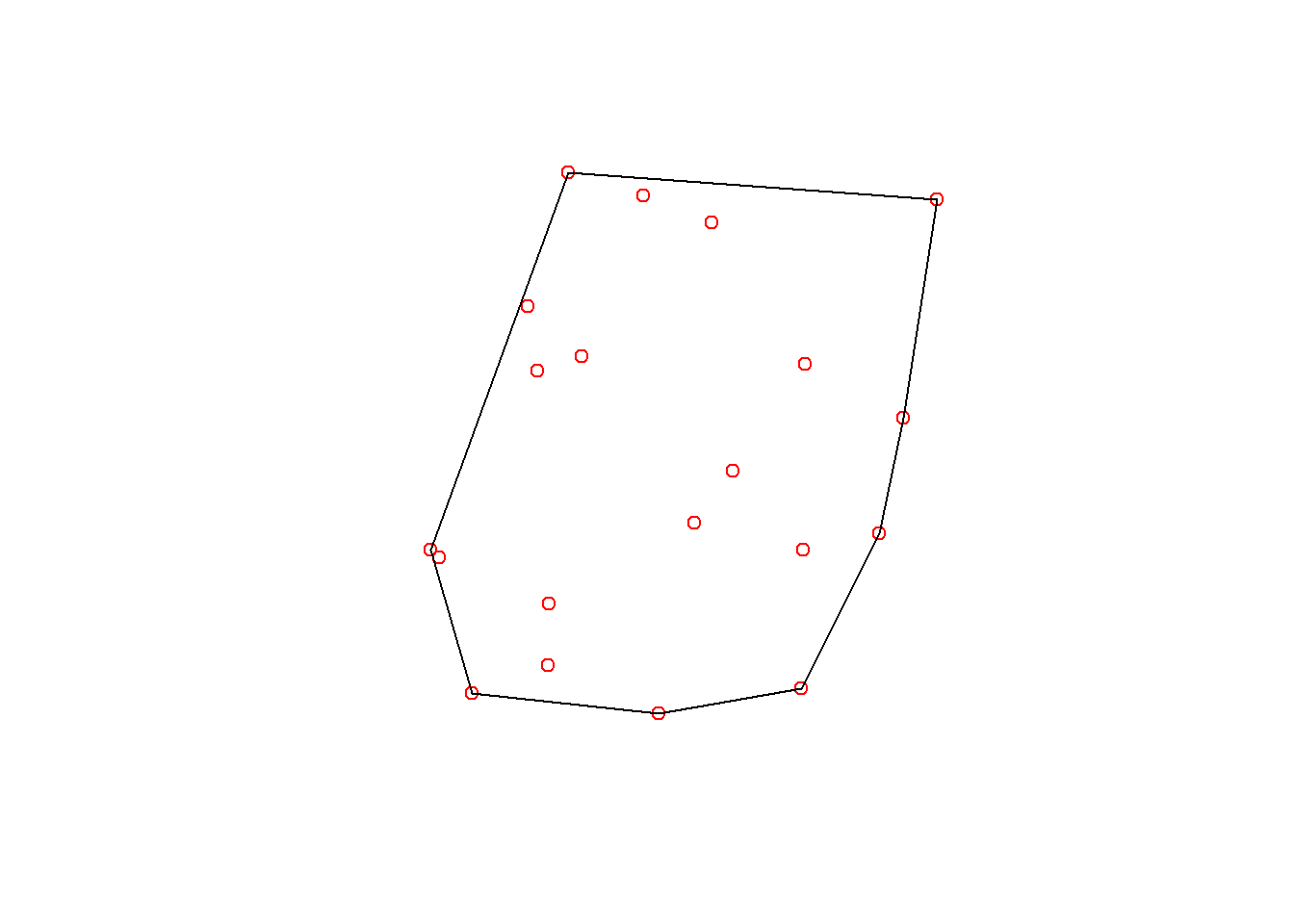
Vínculos espaciales st_join()
Los vínculos de join son diferentes a union, lo que se hace es asociar una variable de una capa a otra capa determinando el valor por su posición geográfica.
Para muchos tipos de análisis se necesita vincular geografías espacialmente. Por ejemplo, si tenemos una capa de puntos con la posición de casas y otra con los polígonos de barrios, podremos con join asignar un nuevo campo o variable a la capa de casas que indique en qué barrio está usando st_join().
Como se trata de vincular columnas de datos la función st_join() requiere datos sf como entrada y no aceptará un objeto que sea solo geometría. Para estos casos hay que transforma la capa con la función st_sf() para convertir objetos de geometría sf en un sf, que es -en definitiva- lo contrario que st_geometry().
# Canarias sola
peninsulaB<-autonomias %>% select(COD_CCAA)%>% filter(COD_CCAA!="04")
# calculo 100 puntos dentro de la peninsula y B
puntos_pen<-st_sample(peninsulaB,size=100)
# pinto las 2 capas
plot(st_geometry(peninsulaB))
plot(puntos_pen, add = T, pch = 16, col = "red")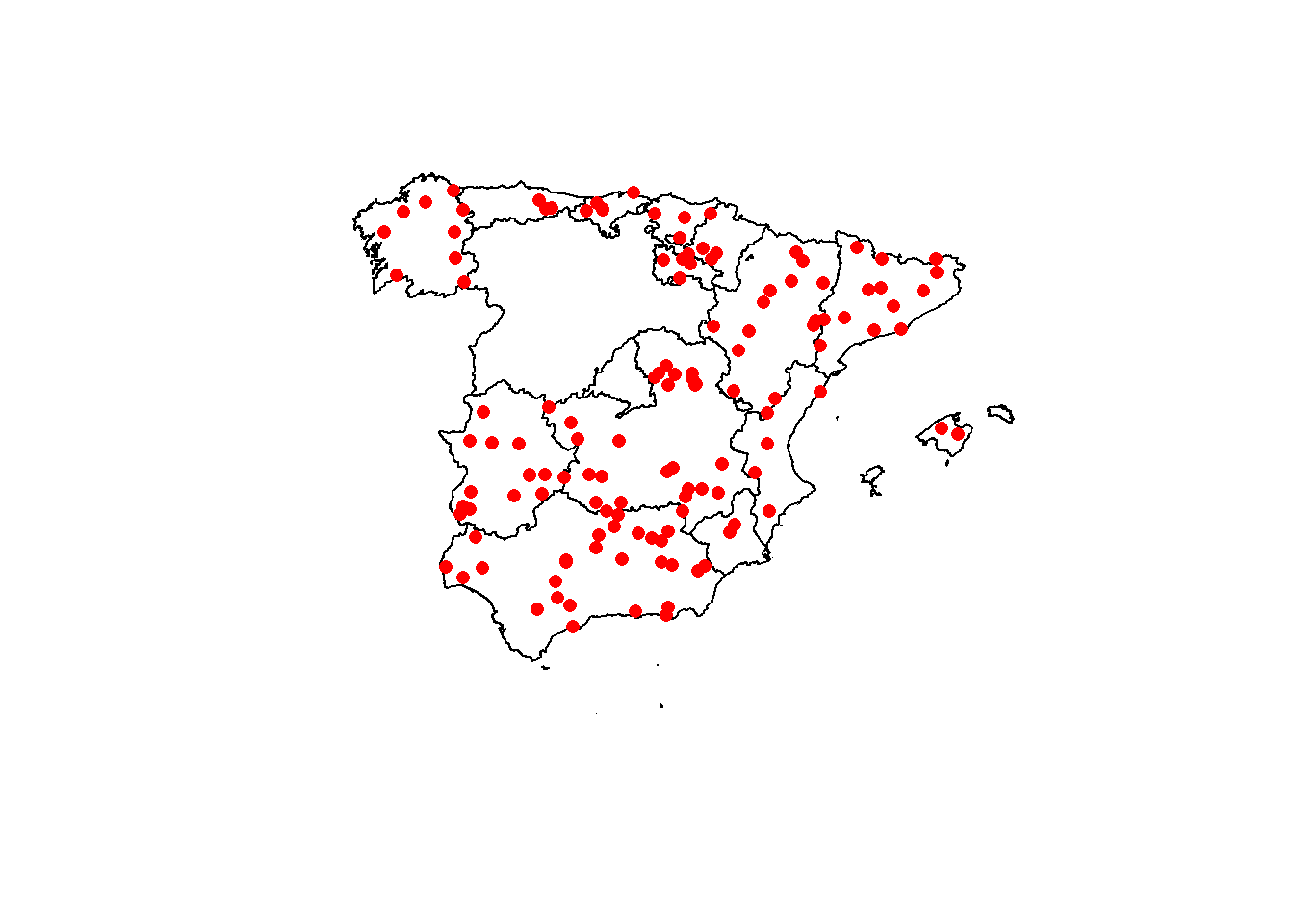
puntos_pen1<-st_union(puntos_pen)
# Determine la clase del los puntos y si es data.frame
class(puntos_pen1) # veo que no## [1] "sfc_MULTIPOINT" "sfc" # Convirto en sf la geometria
puntos_pen2 <- st_sf(puntos_pen1)
# Confirmo que es sf data frame
class(puntos_pen2)## [1] "sf" "data.frame" class(peninsulaB)## [1] "sf" "data.frame" # vinculo ambas capas sf espacialmente
puntosP <- st_join(puntos_pen2, peninsulaB)
# Confirmo que la capa de puntos tienen la informacion de la capa de CCAA
head(puntosP)## Simple feature collection with 6 features and 1 field
## geometry type: MULTIPOINT
## dimension: XY
## bbox: xmin: -8.671461 ymin: 36.55956 xmax: 3.179787 ymax: 43.50636
## epsg (SRID): NA
## proj4string: +proj=longlat +ellps=GRS80 +no_defs
## COD_CCAA geometry
## 1 01 MULTIPOINT (-8.671461 42.84...
## 2 02 MULTIPOINT (-8.671461 42.84...
## 3 03 MULTIPOINT (-8.671461 42.84...
## 4 05 MULTIPOINT (-8.671461 42.84...
## 5 06 MULTIPOINT (-8.671461 42.84...
## 6 08 MULTIPOINT (-8.671461 42.84...Como vemos la función st_join() ha vinculado el campo COD_CCAA de la capa peninsulaB a los puntos de la capa puntos_pen2 y así lo vemos al extraer el encabezado de la tabla.
Contiene e intersecta
Las funciones contiene st_contains() e intersecta con st_intersects() indican como su nombre si una capa espacial está completamente contenida dentro de otra , o si una capa intersecta a otra (en caso de superficies incluye contiene).
Estas dos funciones comprueban relaciones entre dos conjuntos de objetos sf y tienen una salida distinta a otras, pues no dan como resultado una capa, sino una lista de índices.
El resultado de estas y otras funciones relacionadas es un tipo especial de lista. Por ejemplo, cuando se usa st_intersects(A,B), se puede acceder al primer elemento de la salida usando [[1]], que muestra los polígonos de B que se intersecan con A. Del mismo modo, [[2]] mostraría los polígonos del primer polígono A, que se intersecan con el segundo polígono B. Veamos un ejemplo:
# generamos un poligono formado por otros 2
# resultado de dividir un cuadrado por la diagonal
m1 = cbind(c(0, 0, 1, 0), c(0, 1, 1, 0))
m2 = cbind(c(0, 1, 1, 0), c(0, 0, 1, 0))
# transformamos en una lista sf los 2 pol
pol0 = st_sfc(st_polygon(list(m1)), st_polygon(list(m2)))
pol<-st_sf(pol0)
zona<-st_union(pol)
# pintamos los dos poligonos
plot(st_geometry(pol))
text(x=c(0.25,0.75), y=c(0.75,0.25), labels = 1:2)
# generamos 5 puntos
p5<-st_sample(zona,size=5)
plot(p5,pch = 5,lwd=5, add = TRUE)
# generamos un capa de bufer
p5_buffer<-st_buffer(p5,dist=0.1)
plot(p5_buffer, add = TRUE)
# bufer contenido en rectanguno
vecinos_cont <- st_contains(zona,p5_buffer)
cont <- vecinos_cont[[1]]
plot(p5_buffer[cont], add = TRUE, col = scales::alpha("yellow", 0.4))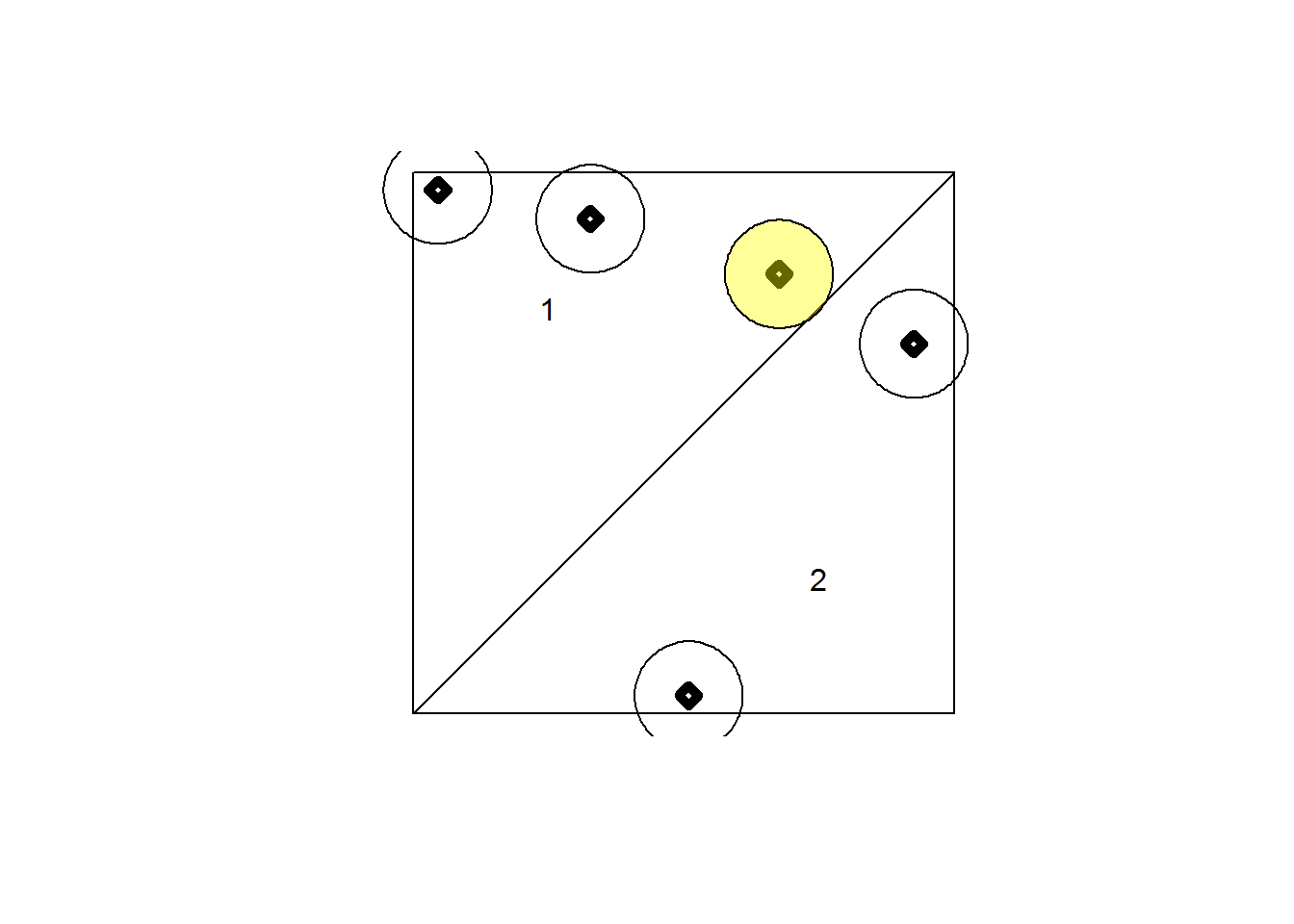
Veamos ahora un ejemplo de intersección:
zona<-pol0[[1]]
plot(zona, col="grey")
plot(p5,pch = 5,lwd=5, add = TRUE)
plot(p5_buffer, add = TRUE)
# bufer contenido en poligono
vecinos_inter <- st_intersects(zona,p5_buffer)
inter <- vecinos_inter[[1]]
plot(p5_buffer[inter], add = TRUE, col = scales::alpha("yellow", 0.4))
# recortamos con clip
vecinos_clip <- st_intersection(p5_buffer, zona)
plot(vecinos_clip, add = TRUE, col = scales::alpha("red", 0.5))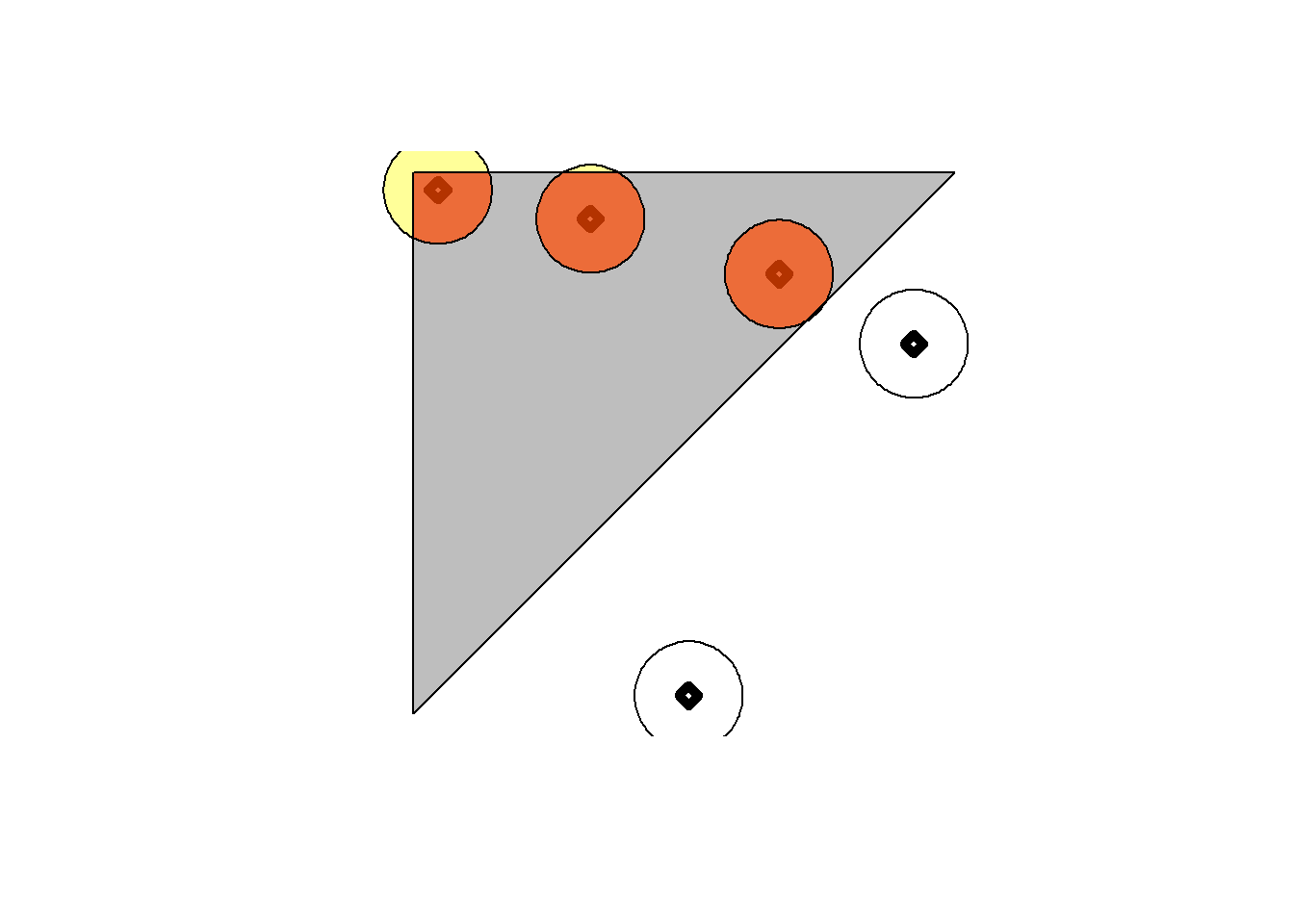
Distancias
Medir la distancia entre objetos es una parte importante de muchos análisis espaciales. Existen varias funciones en R base, así como en los paquetes rgeos y geosphere para calcular distancias, pero la función st_distance() de sf proporciona una matriz de distancia bastante completa que puede utilizarse para la mayoría de las necesidades.
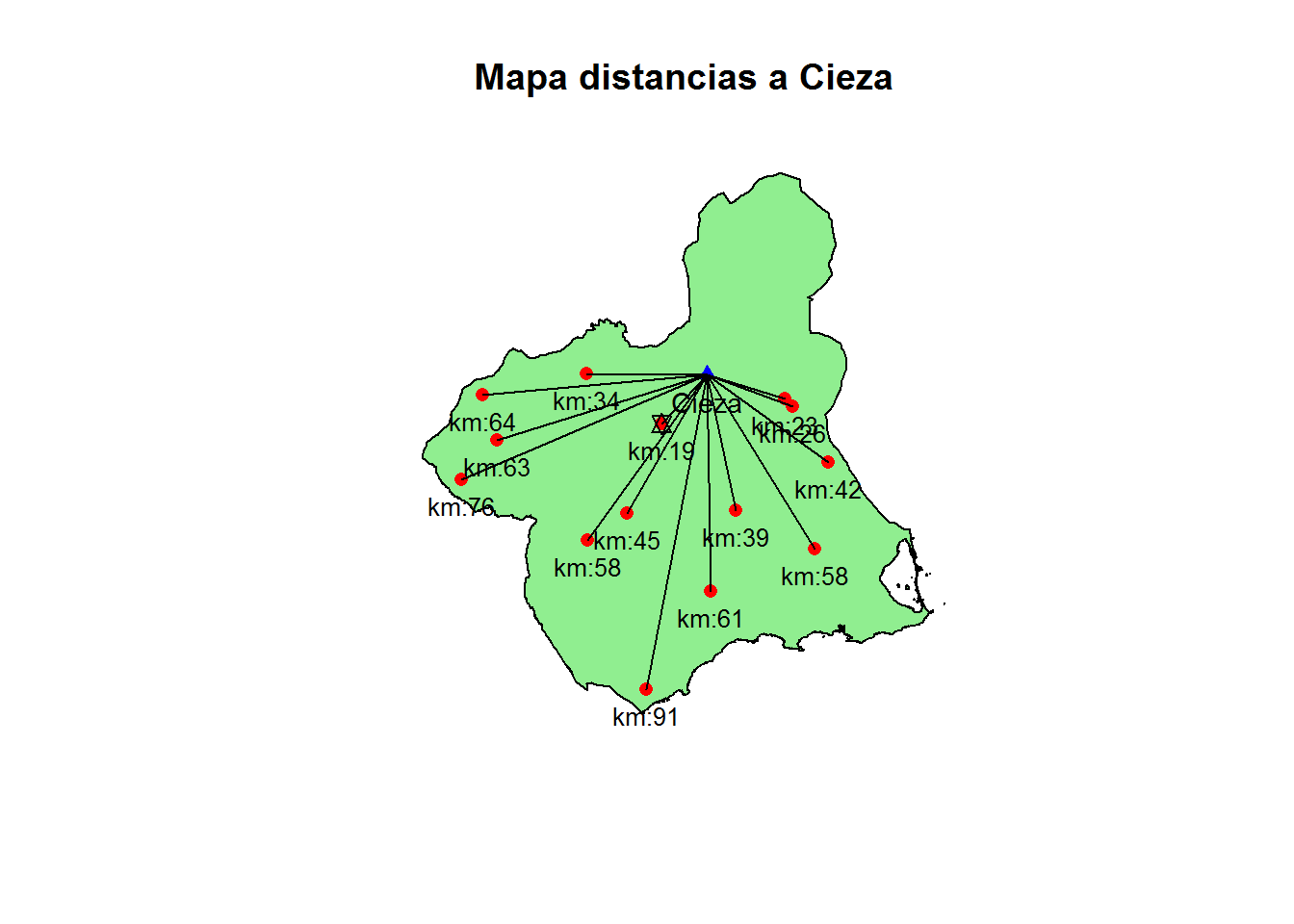
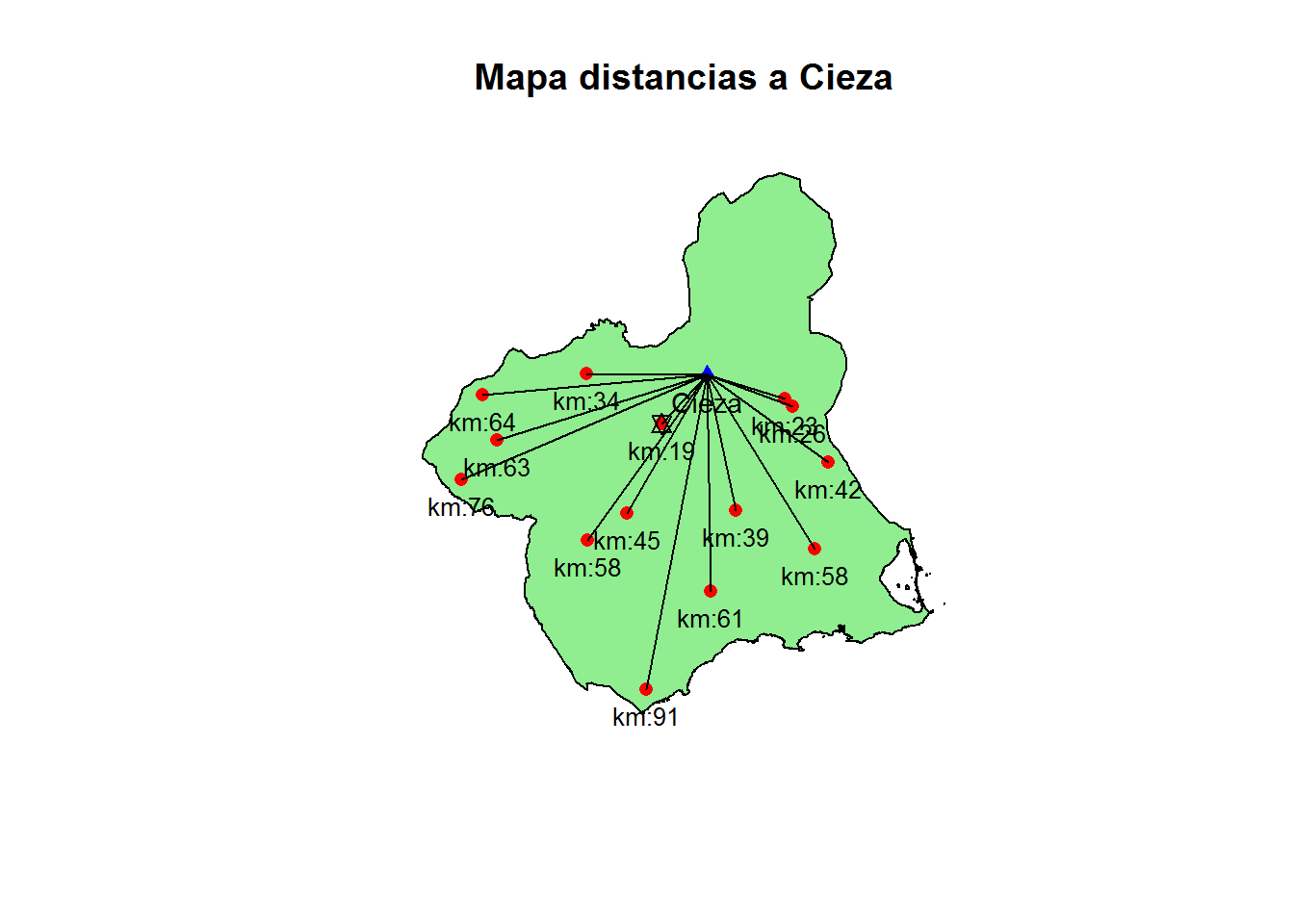
En este ejercicio, vamos a generar puntos aleatorios dentro del mapa de la Región de Murcia y calcular la distancia de esos puntos al municipio de Cieza.
# Murcia sola
Murcia<-autonomias %>% select(COD_CCAA)%>% filter(COD_CCAA=="15")
# Establecemos su epsg, ya que la capa no lo define
st_crs(Murcia) = 4326
# calculo 10 puntos dentro de Murcia
puntos_mur<-st_sample(Murcia,size=10)
# creo un punto sf con los datos de Cieza
p_cieza<- data.frame(lon=-1.42, lat= 38.24)
p_cieza <- st_as_sf(p_cieza, coords = c("lon", "lat"))
# les asigno sistema de coordenadas
st_crs(p_cieza) =4326
st_crs(puntos_mur) =4326
#st_transform(puntos_mur, crs = st_crs(Murcia))
# pinto las capas
plot(st_geometry(Murcia), col="lightgreen", main="Mapa distancias a Cieza")
plot(p_cieza, add = T, pch = 17, col = "blue",lwd=5)
text(st_coordinates(p_cieza),
labels = "Cieza",
pos=1,cex=0.9)
plot(puntos_mur, add = T, pch = 16, col = "red")
# calculamos las distancias
d <- st_distance(p_cieza, puntos_mur)
head(d)## Units: [m]
## [1] 25985.51 42328.64 19119.80 90853.35 58139.53 39268.75 # calculamos el mas cercano
mascercano <- which.min(d)
plot(puntos_mur[mascercano], add = T, pch = 11, col = "black")
prueba1<-st_cast(st_union(puntos_mur,p_cieza),"LINESTRING")
plot(prueba1,add=T)
text(st_coordinates(puntos_mur),
labels = paste0("km:",round(unclass(d)[1,]/1000,0)),
pos=1,cex=0.8)