Algoritmo golfo cabo
Hace unas semanas escribí un artículo de cómo generar un polígono de isla aleatoria, después lo complementamos con habilidades gráficas para crear una aplicación que hace mapas del tesoro aleatorios con varias islas y muchos adornos, lo puedes ver aquí.
Cuando estuve programando el mapa del tesoro busqué un algoritmo que ayudara a localizar los puntos en el perímetro que fueran cabos y los puntos que fueran bahías o golfos, con la idea de poner nombres a estos puntos singulares, para que el mapa fuera realista.
Al final, lo que hice fue aplicar un simplify fuerte (st_simplify()) al polígono con la opción de mantener topología. Esto detecta con bastante acierto los puntos singulares, pero no me dice cuáles son cabos o bahías.
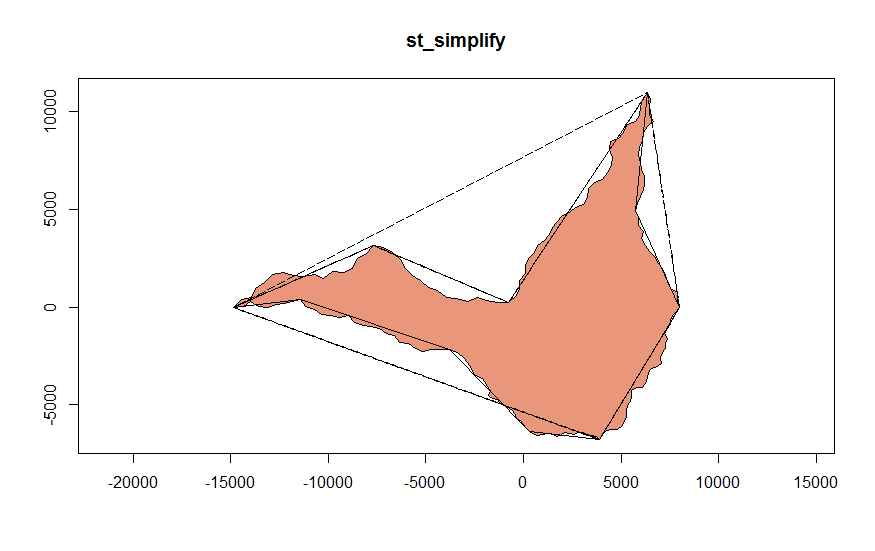
simplify poligono origen
El caso es que no le dediqué mucho más tiempo, y tampoco encontré nada en la web para detectar cabos y golfos, pero hace unos días me vino una idea a la cabeza para detectarlos que he puesto en práctica y funciona muy bien.
Este artículo voy a exponer esa idea y la programación en R del algoritmo. Aunque ha sido totalmente original, agradecería si algún lector conoce alguna solución alternativa simplificada.
Idea
Es bastante simple, se trata de detectar si un punto de una línea de costa es más cabo que golfo y lo haremos pintando un circulo en cada punto del perímetro y calculando el área que interseca con la tierra. La división del área intersecada con la total nos da un valor entre 0 y 1. Cuanto más cerca de 1, el punto está más abrigado por tierra y será por tanto un golfo, cuanto más cerca de 0 el punto está menos abrigado y será un cabo.
Es decir, obtendremos para cada punto de la línea de costa, un valor normalizado que nos distingue entre golfo y cabo.
Algoritmo golfo-cabo de VilBer:
- dividir la línea de costa en puntos.
- en cada punto trazar un círculo de radio R. El radio debe ser de amplitud similar a las bahías que se desea detectar.
- Hallar la intersección del círculo con la línea de costa y calcular el área intersecada A1.
- Dividir A1 entre el área del círculo completo.
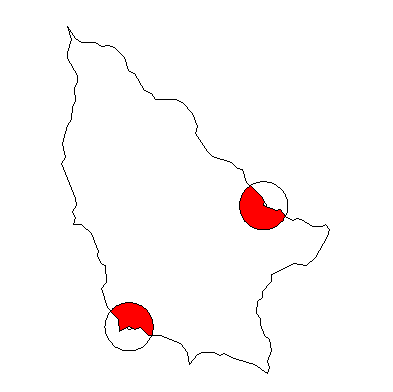
Ejemplo de algoritmo golfo cabo de Vilber en dos puntos
Desarrollo en R
El algoritmo va a crear en cada punto del contorno de la isla un círculo de radio= r y calcular el área de la superficie que interseca con la isla.
Hemos programado 2 funciones para hacer el trabajo: por_circulo(), que calcula el tanto por uno de área intersectada por el círculo con la parte de tierra, y gc(), que calcula esto para cada punto de la línea de costa y da como resultado una capa sf con los valores por punto en la columna gc.
Nota: he usado sapply en lugar de un bucle pues son funciones mucho más rápidas.
# Funcion por_circulo:
# Calcula el área de interseccion del circulo con elpoligono de tierra de la isla
# punto: punto del contorno
# isla: poligon de tierra o de la isla sf
# tolerancia: radio del circulo
por_circulo<-function(punto,isla,tolerancia){
# crea un circulo de radio=tolerancia
cir1<-st_buffer(st_geometry(punto),dist=tolerancia)
# calcula su área
area_circulo<-as.numeric(st_area(cir1))
# clip con tierra-isla
# iguala los crs para evitar conflictos
st_crs(cir1)<-st_crs(isla)
# hace el clip del circulo con la tierra-isla
clip1 <- st_intersection(cir1,isla)
# calcula el area del clip
area_cir1<-as.numeric(st_area(clip1))
# retorna el tanto por uno
return(area_cir1/area_circulo)
}
# funcion algoritmo golfo cabo
# isla: sf con poligono cerrado de tierra
# R: radio del circulo = tolerancia
# seg: unidades para segmentar la linea de costa
gc<-function(isla,radio=2000){#},seg=200){
# unidades en m
# segmentiza la linea de costa
# crea un punto cada 200 m maximo
#c1<-st_segmentize(st_geometry(isla),seg)
c1<-isla
# convierte la capa a puntos
pts_c1<-st_cast(c1, "POINT")
# calcula el algoritmo con sapply en cada punto
gc1<-sapply(pts_c1,por_circulo,isla=c1,tolerancia=radio)
gc1<-as.data.frame(gc1)
names(gc1)<-c("gc")
# genera una capa sf de resultado con los puntos y los valores
pts_c2<-st_sf(gc1, st_geometry(pts_c1))
#retorna el resultado como capa
return(pts_c2)
}
# funcion para calcular los puntos que salen en una capa de lineas
n_puntos<-function(poli){
# numero de puntos de una capa
pts_poli<-st_cast(poli$geometry, "MULTIPOINT")
cnt_poli <- sapply(pts_poli, length)
sum(cnt_poli)
}También hay una función n_puntos, que es meramente informativa, con los puntos que salen de la capa, para comparar como simplifica st_simplify.
Manos a la obra: vamos a generar una isla aleatoria, usando las funciones del artículo de mapa del tesoro:
# generamos una isla
radio=8000
islagrande<-crea_isla(R=radio)%>% pol_to_sf() #%>%validar_contorno()
plot(islagrande, col="darksalmon", main="Isla ejemplo")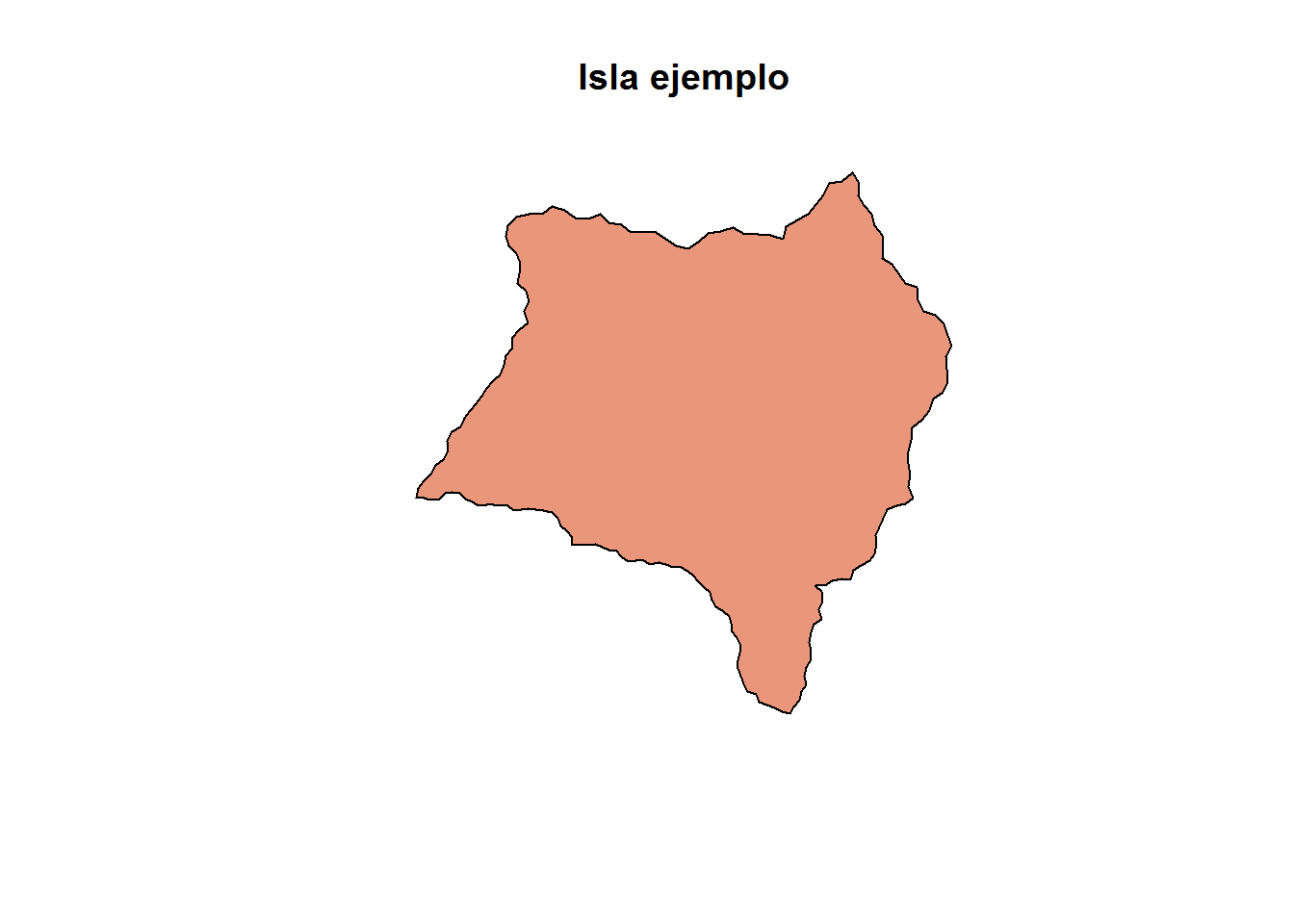
Identificar cabos y golfos principales
A partir de esta isla aleatoria, lo primero que haremos es aplicar un st_simplify, lo que nos identifica ya unos puntos clave que hay que identificar como cabos y golfos.
A esta capa simplificada le aplicamos el algoritmo golfo cabo y obtenemos unos valores en la columna gc, que como explicamos identifica si es un cabo o un golfo según su valor esté cerca de 0 (cabo) o cerca de 1 (golfo).
# Simplificamos el poligono origen
i1<-st_simplify(islagrande, preserveTopology = FALSE, dTolerance = 1000)
# comparamos los puntos de ambas capas
n_puntos(i1)## [1] 22 n_puntos(islagrande)## [1] 386# calculamos el algoritmo en la capa simplificada
a<-gc(i1)
# Vemos el resultado.
head(a)## Simple feature collection with 6 features and 1 field
## geometry type: POINT
## dimension: XY
## bbox: xmin: -8006.278 ymin: -6967.381 xmax: 8000 ymax: 5647.622
## epsg (SRID): NA
## proj4string: NA
## gc st_geometry.pts_c1.
## 1 0.4061323 POINT (8000 0)
## 2 0.6021625 POINT (4853.172 -2822.559)
## 3 0.1328132 POINT (4022.619 -6967.381)
## 4 0.6077783 POINT (528.2558 -2241.867)
## 5 0.2006587 POINT (-8006.278 9.804538e-13)
## 6 0.6069260 POINT (-4410.982 5647.622)# pintamos el resultado
plot(st_geometry(islagrande), col="lightgrey")
plot(st_geometry(a),add=T)
plot(a[a$gc>0.5,],pch=19,cex=2, col="red",add=T)
plot(a[a$gc<0.5,],pch=16,cex=2, col="blue",add=T)
# señalamos el golfo más evidente
plot(a[which.max(a$gc),],pch=0,cex=2, col="red",add=T)
text(st_coordinates(a[which.max(a$gc),]), labels = "playa", col = 'red',pos = 4)
# señalamos el cabo más evidente
plot(a[which.min(a$gc),],pch=0,cex=2, col="blue",add=T)
text(st_coordinates(a[which.min(a$gc),]), labels = "cabo", col = 'blue',pos = 4)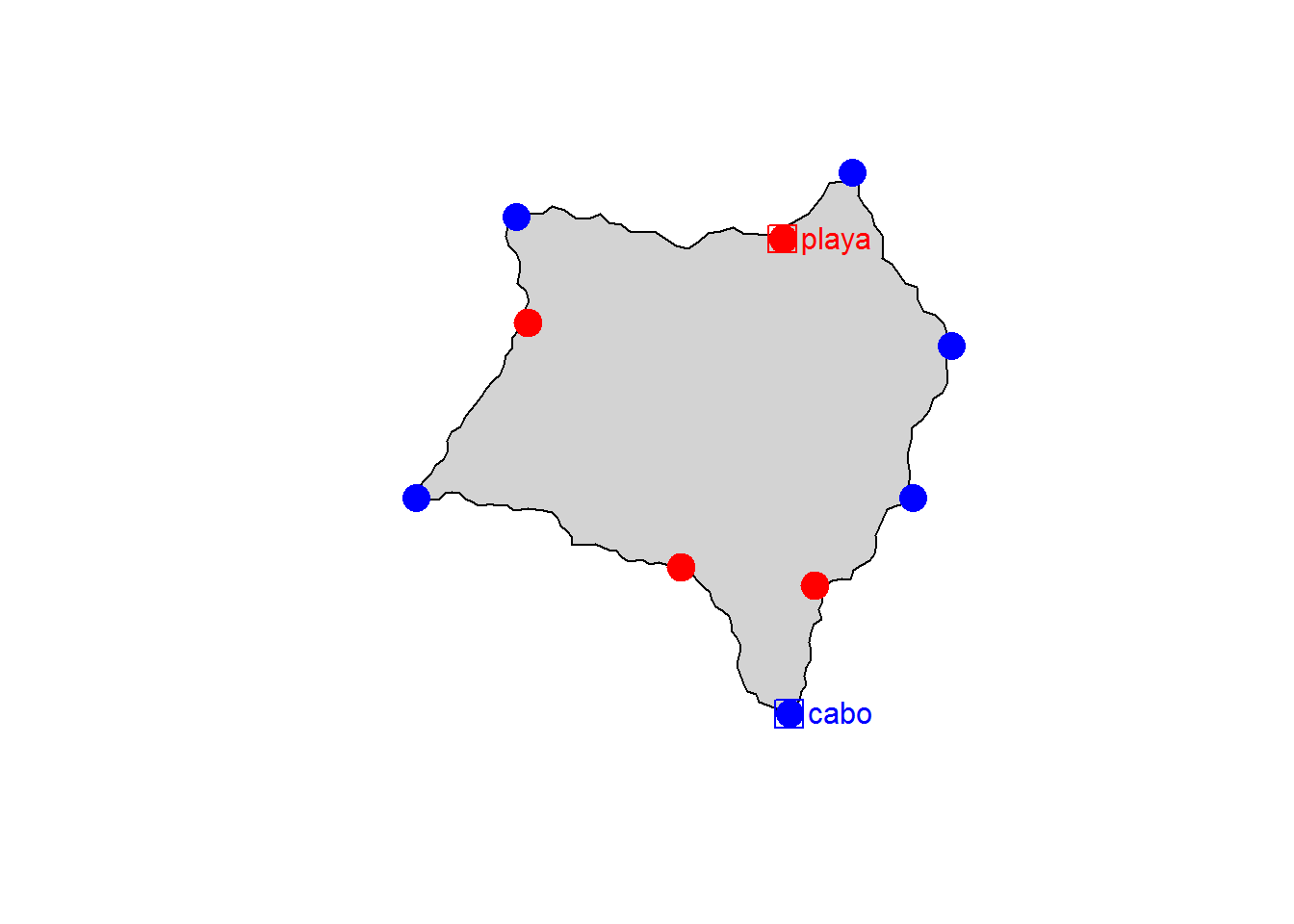
Aplicar a todo el perímetro
Si buscamos no identificar los cabos y golfos principales, sino saber que tendencia tiene cada punto del perímetro, aplicaremos el algoritmo a la capa origen.
En este ejemplo hacemos además una amplificación del grosor del punto.
a<-gc(islagrande)
# pintamos el resultado variando el color,el grueso del punto
# y las escalas
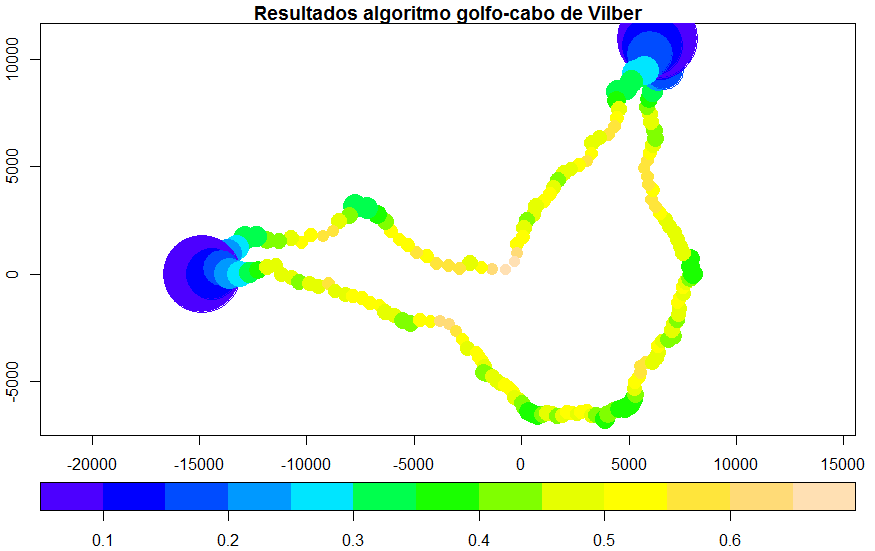
plot(a["gc"],key.pos = 1,pch=19,main="Resultados algoritmo golfo-cabo de Vilber",
pal=topo.colors,cex=(1/a$gc),axes = T, key.width = lcm(2), key.length = 1.0) 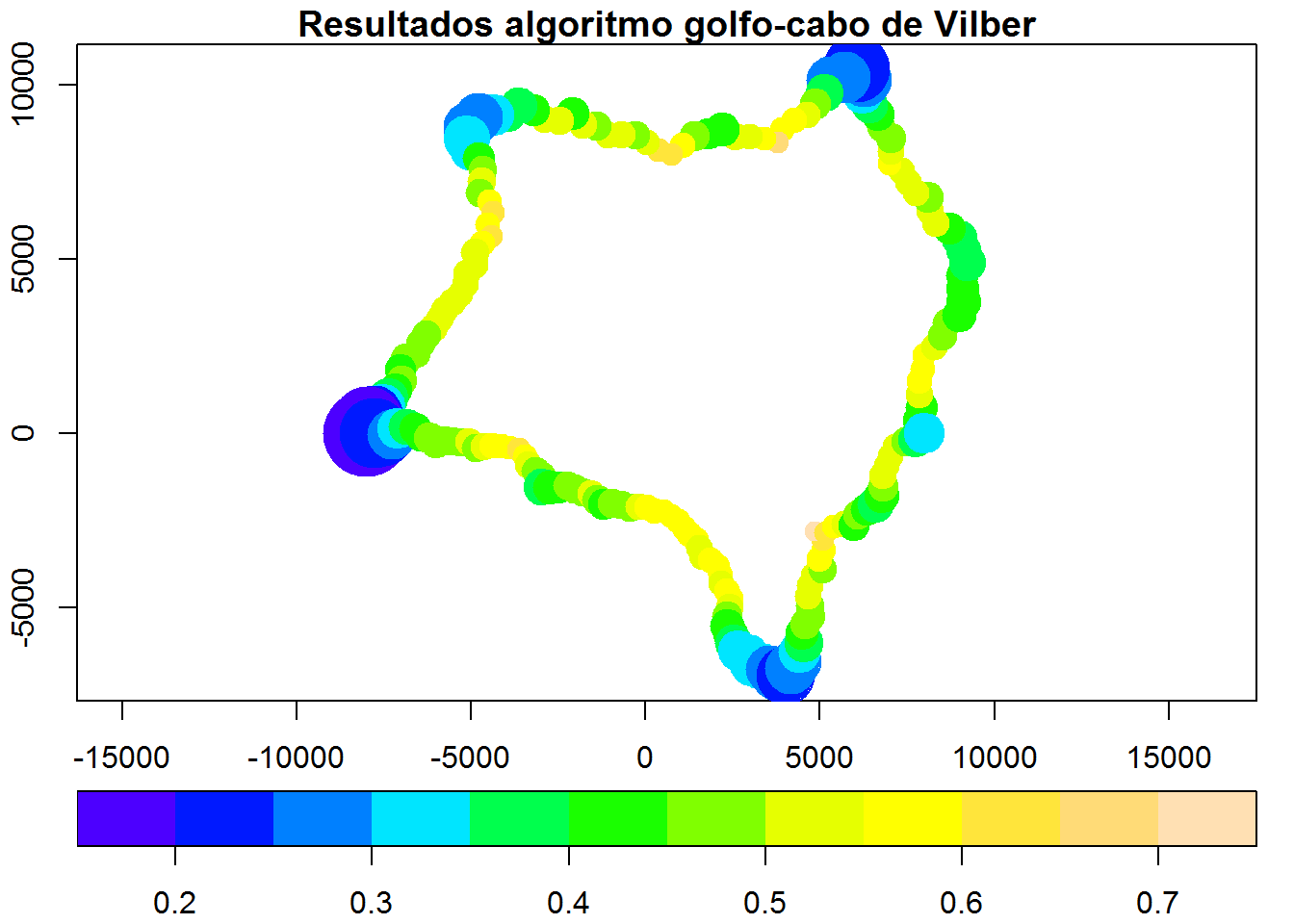
Los resultados gráficos muestran que la función es bastante acertada y permite reconocer fácilmente las zonas de cabos y las playas en golfos o bahías de la isla.
Una forma alternativa de ver los resultados podría ser limitando la escala con breaks y así delimitar cada zona:
# zona playa y cabo
plot(a["gc"],key.pos = 1,pch=19,main="zona playa-cabo",breaks = c(0,.25,.50,1), axes = T, key.width = lcm(2), key.length = 1.0) 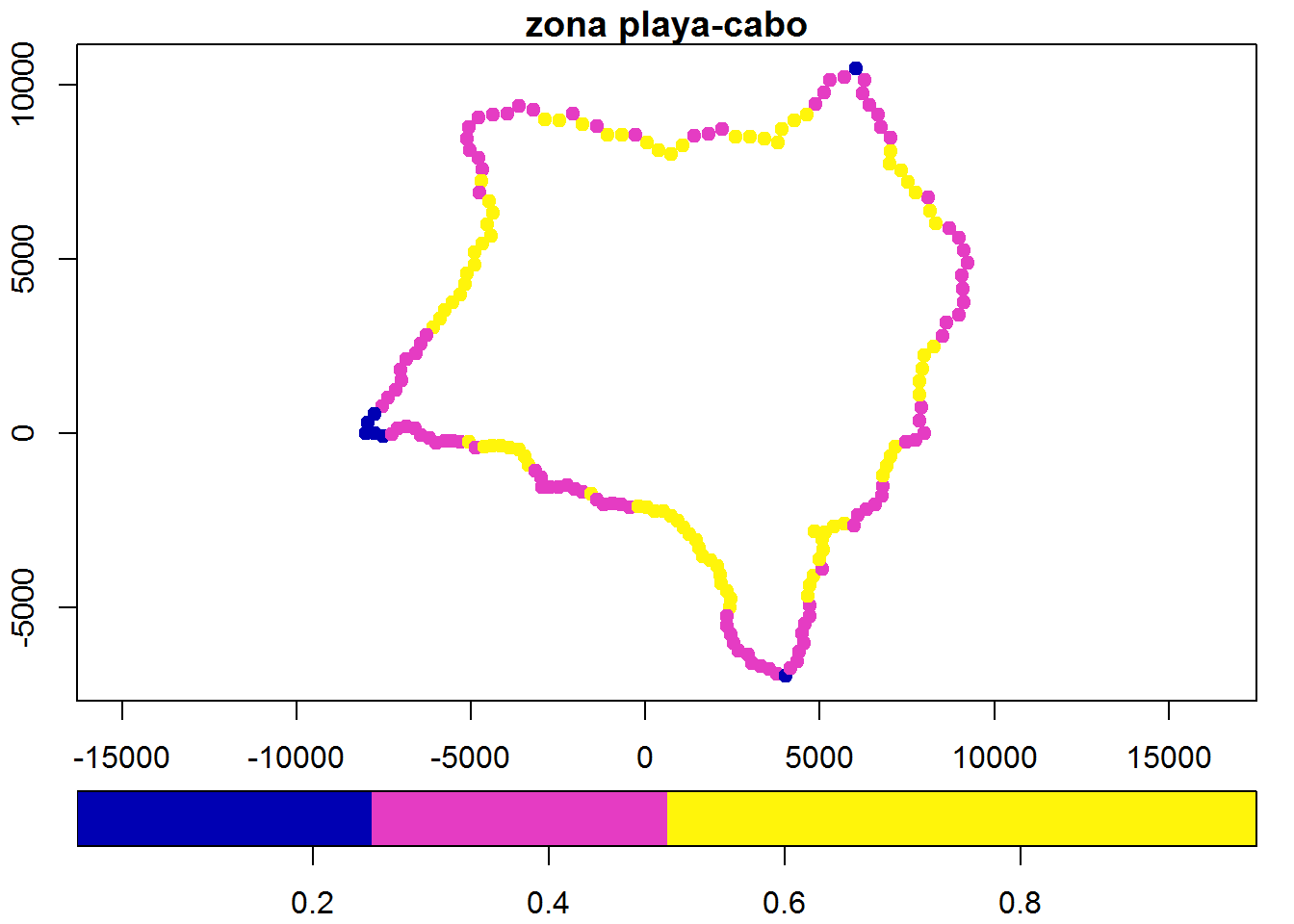
ggplot
Otra interpretación gráfica interesante se puede hacer con ggplot, con el grosor de línea variable según el índice gc. En este caso, la línea gruesa indica cabo, la fina bahía.
library(ggplot2)
#CReamos un data frame
aux<-data.frame(st_coordinates(a),a$gc)
# cambiamos los nombres
names(aux)<-c("x","y","z")
# pintamos la ruta
ggplot(aux, aes(aux$x,aux$y,size=(1/aux$z))) +
geom_path(linejoin = "round",lineend="round")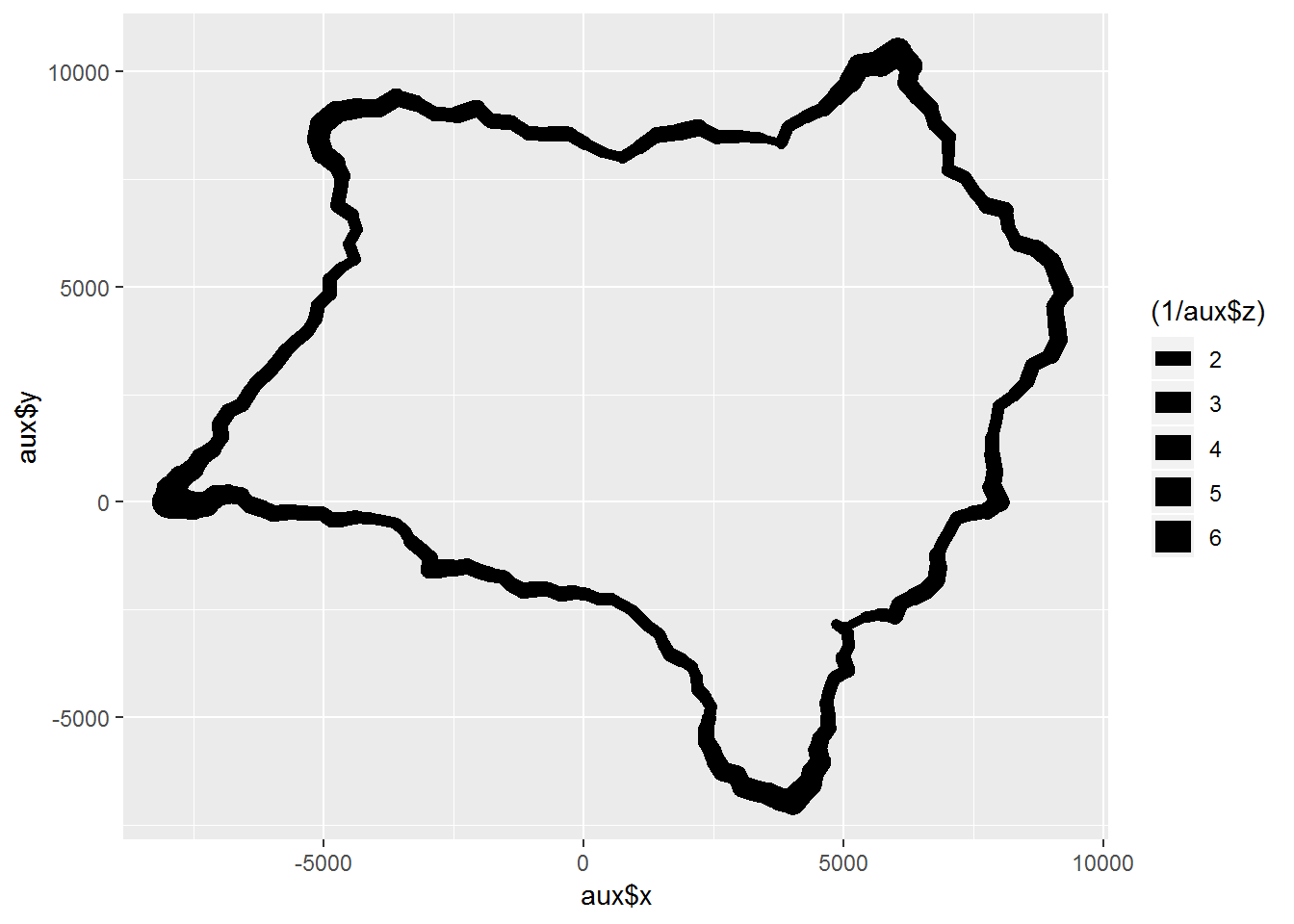
Resultados para diferentes radios
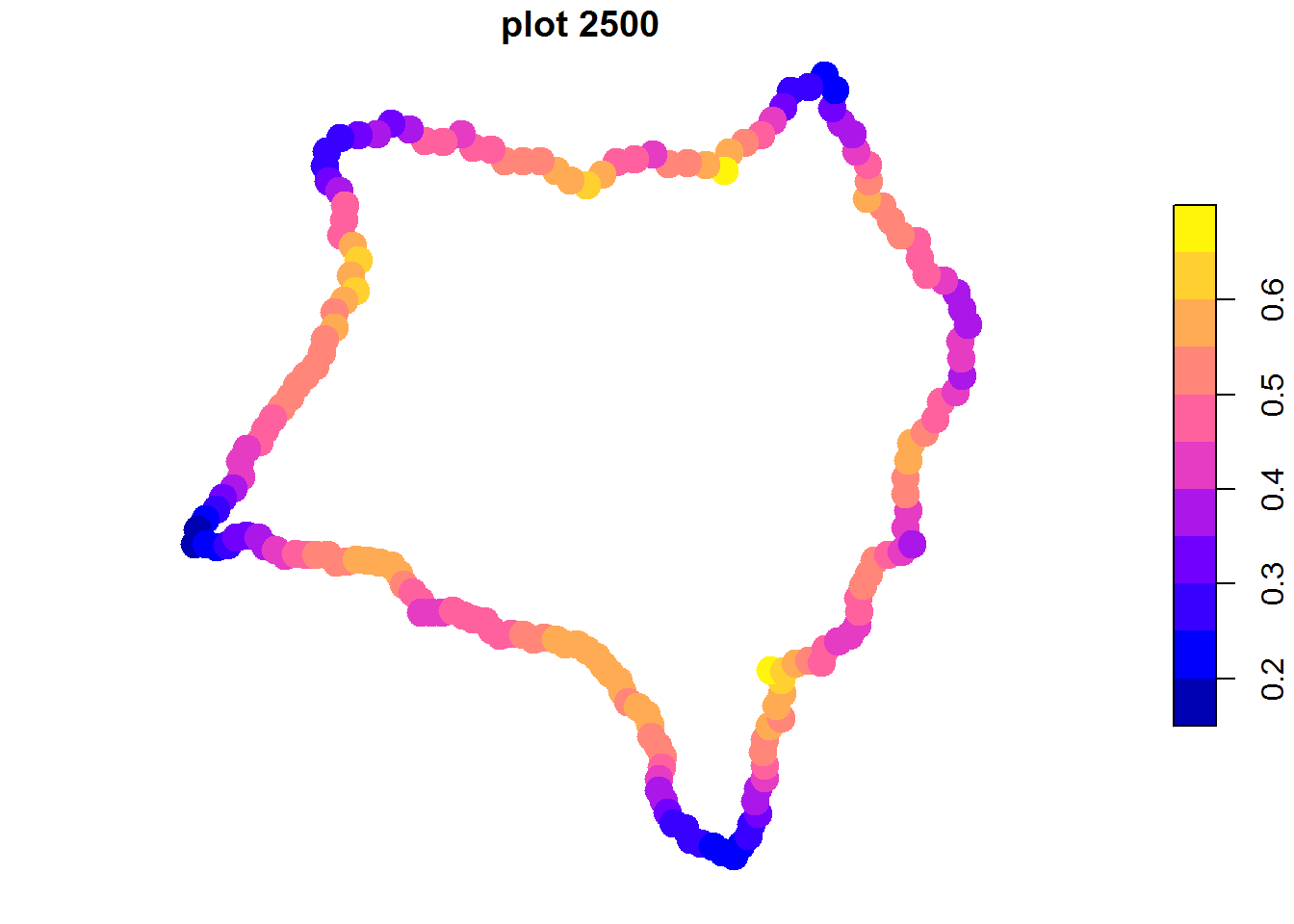
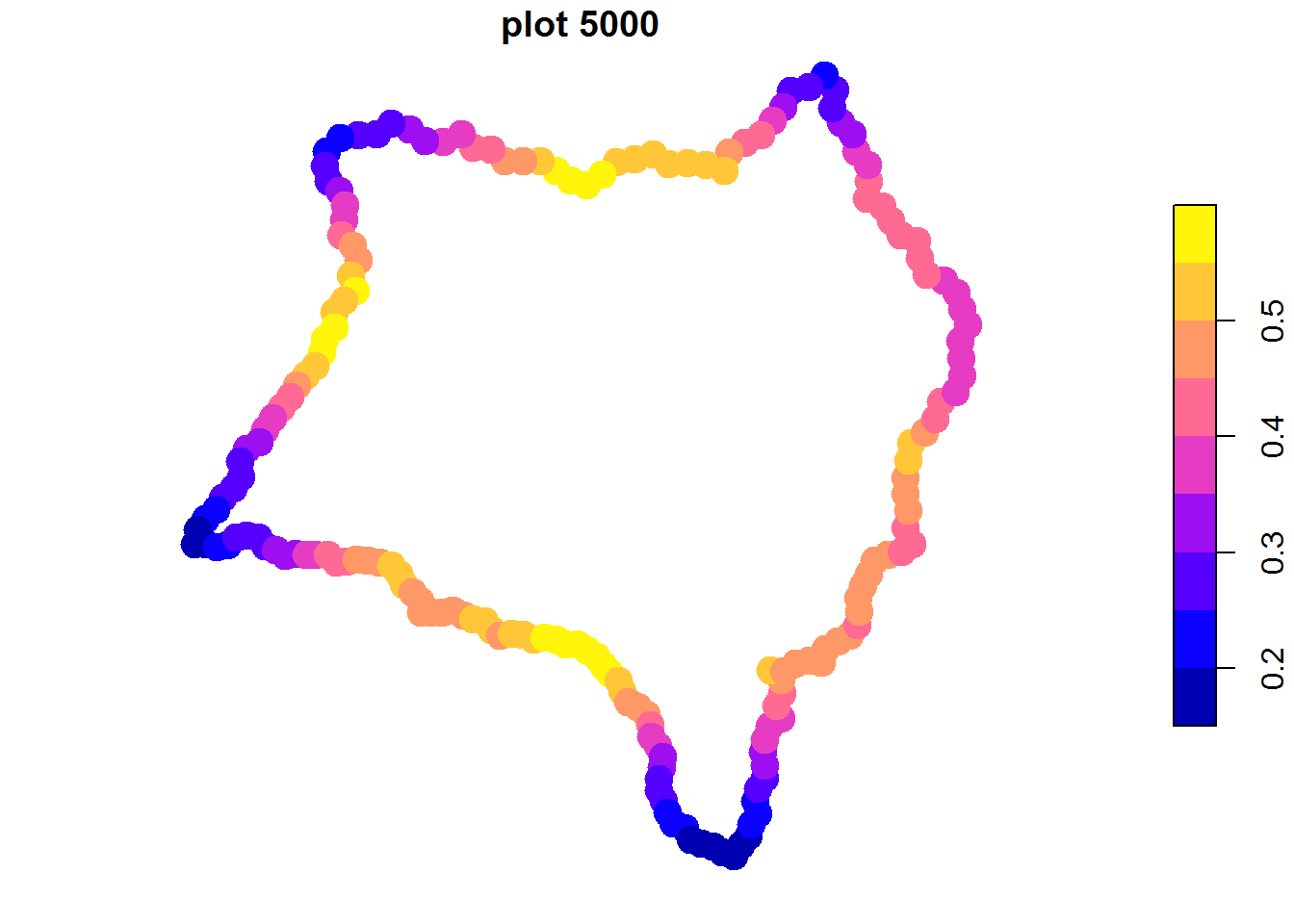
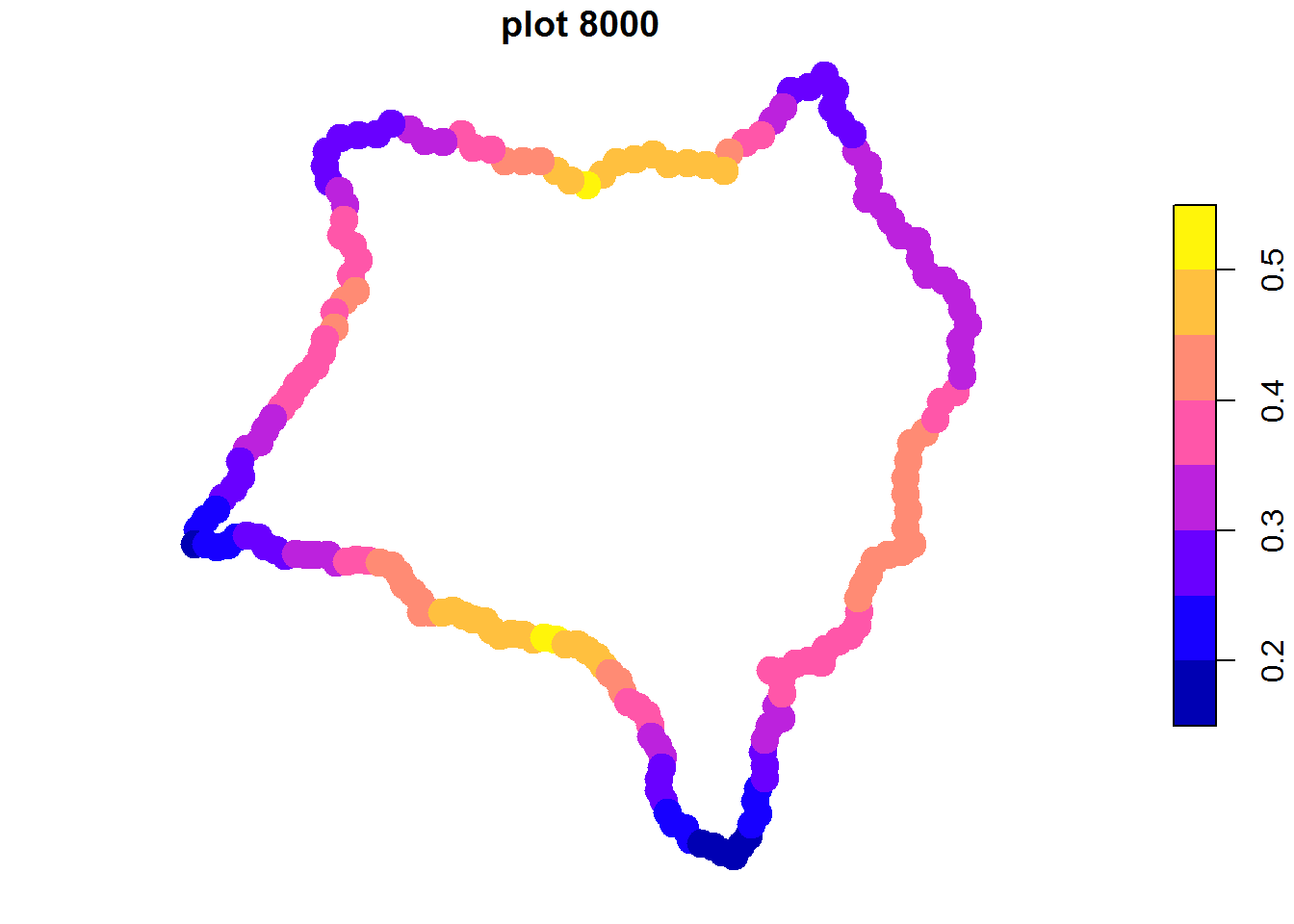
El radio del círculo es importante en la determinación de las zonas, debe elegirse una magnitud representativa del tamaño de playa buscado, es decir, del mismo orden de magnitud que la longitud de playa.
Vamos a hacer una comparación con 4 valores de radio:
# pintamos con varios radios
radios<-list(1000, 2500, 5000, 8000)
#. aplicamos el bucle
pl<-lapply(radios, function(x) {plot(gc(islagrande,radio=x),pch=19,cex=2,
main=paste("plot", x[[1]]))})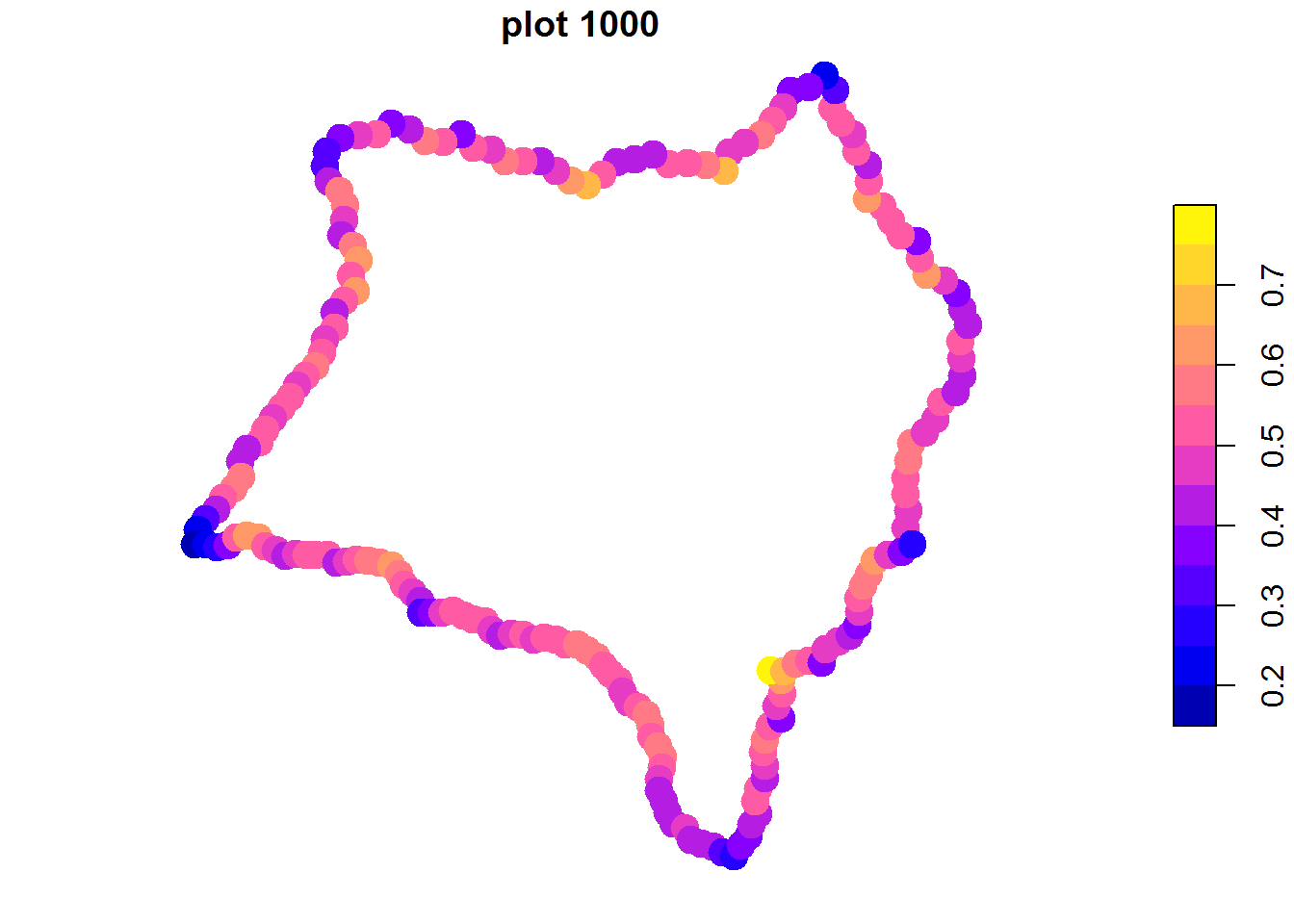
#knitr::include_graphics(pl)Conclusiones
Este algoritmo es muy interesante, y creo que se puede extender de una forma más global. Por ejemplo, si pensamos en 3D haríamos lo mismo, pero con una esfera en lugar de un círculo y nos daría un índice de convexidad - concavidad del terreno.
También puede pensarse como indicador para series temporales, en este caso haciendo un medio círculo en el punto actual de dato, y calculando el porcentaje de área pasada que intersecta el círculo….

