Series temporales con arima II
El anterior post fue una introducción a los modelos ARIMA, ahora vamos a ver ejemplos prácticos.
Recuerda que es importante saber interpretar las gráficas de los correlogramas ACF y PACF que nos dan el orden del modelo según esta guía:
| AR(p) | MA(q) | ARMA(p,q) | |
|---|---|---|---|
| ACF | varios puntos con coef>0 decayendo | 0 excepto los q primeros |
varios puntos con coef>0 decayendo |
| PACF | 0 excepto los p primeros |
varios puntos con coef>0 | varios puntos con coef>0 |
Utilizaremos principalmente las librerías astsa y forecast cada una tiene unas funciones para hacer el proceso. Además veremos de pasada otras como tseries que tiene buenas funciones para limpiar y detectar outliers, o quitar NA de los datos como la función tsclean.
Ejemplo 1. Manchas solares
La serie temporal sunspot.year contiene la secuencia con el número de manchas solares observadas cada año entre 1700 y 1988. Estos datos junto con muchos otros vienen de ejemplo en \(R\) con la librería datasets.
# cargamos las librerías
library(astsa)
library(forecast)
library(ggplot2)
# Observamos la serie temporal y correlogramas
ggtsdisplay(sunspot.year, main="manchas solares") 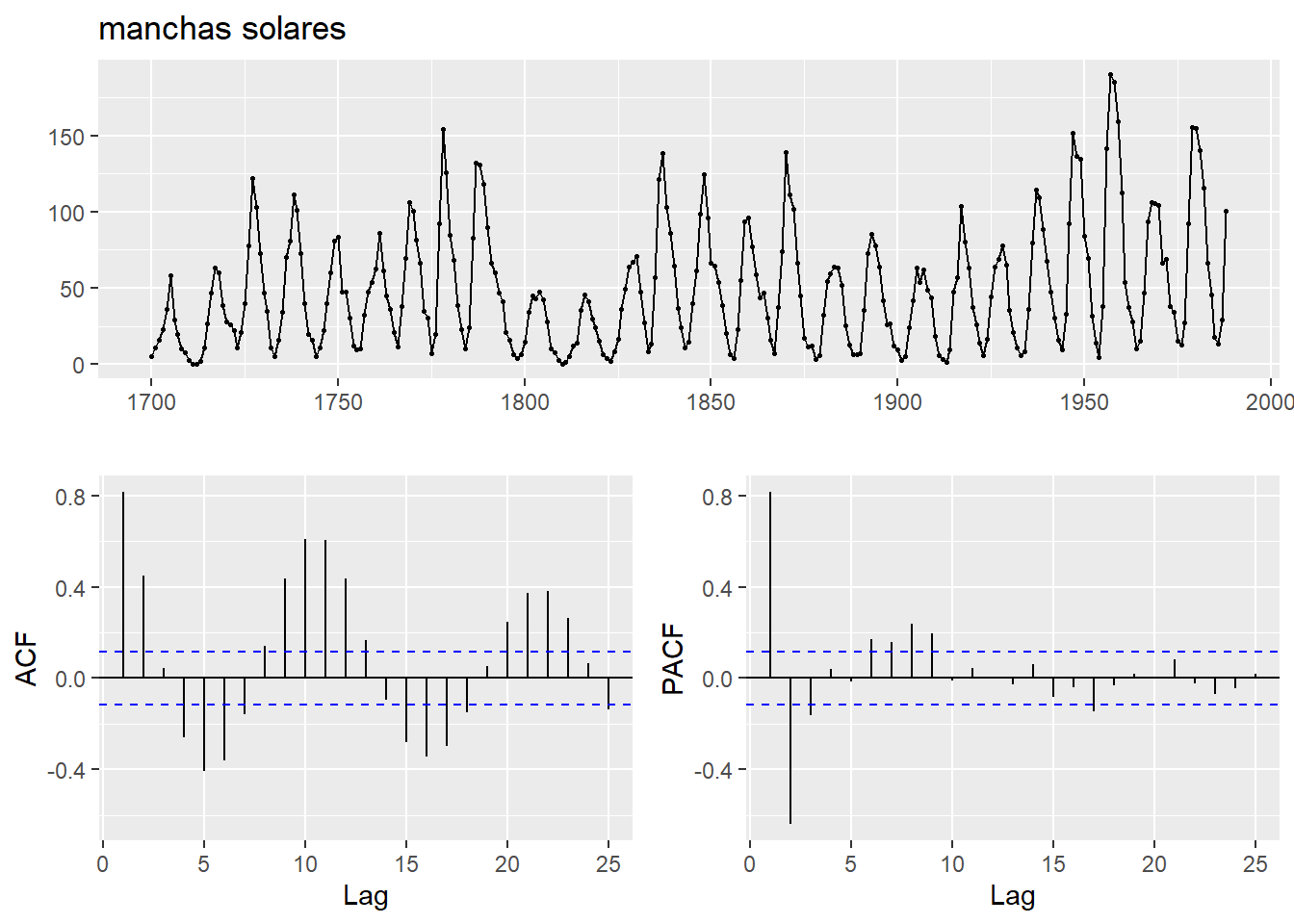
La gráfica nos muestra una serie sin tendencia, pero con ciclos por lo que NO es estacionaria. En una visión más detallada vemos que estos ciclos no son constantes en periodo, y que varía aleatoriamente entre los 6,7,8,9 o 17 años.
Ejecutamos las funciones ndiffs para ver si hay que diferenciar (que parece que si) y si encuentra ciclo estacional.
# estimacion de I(d) y (D)
ndiffs(sunspot.year)## [1] 1#nsdiffs(sunspot.year) # si da error es que no hay cicloEl resultado de la función ndiffs() es uno, por lo que d=1, hay que diferenciar, pero que no encuentra periodo estacional D con nsdiffs que da error. Al indicarnos que es un I(d=1), tenemos que pintar la gráfica de la serie diff()para estimar los posibles órdenes ARMA(p,q):
ggtsdisplay(diff(sunspot.year), main="diff de manchas solares")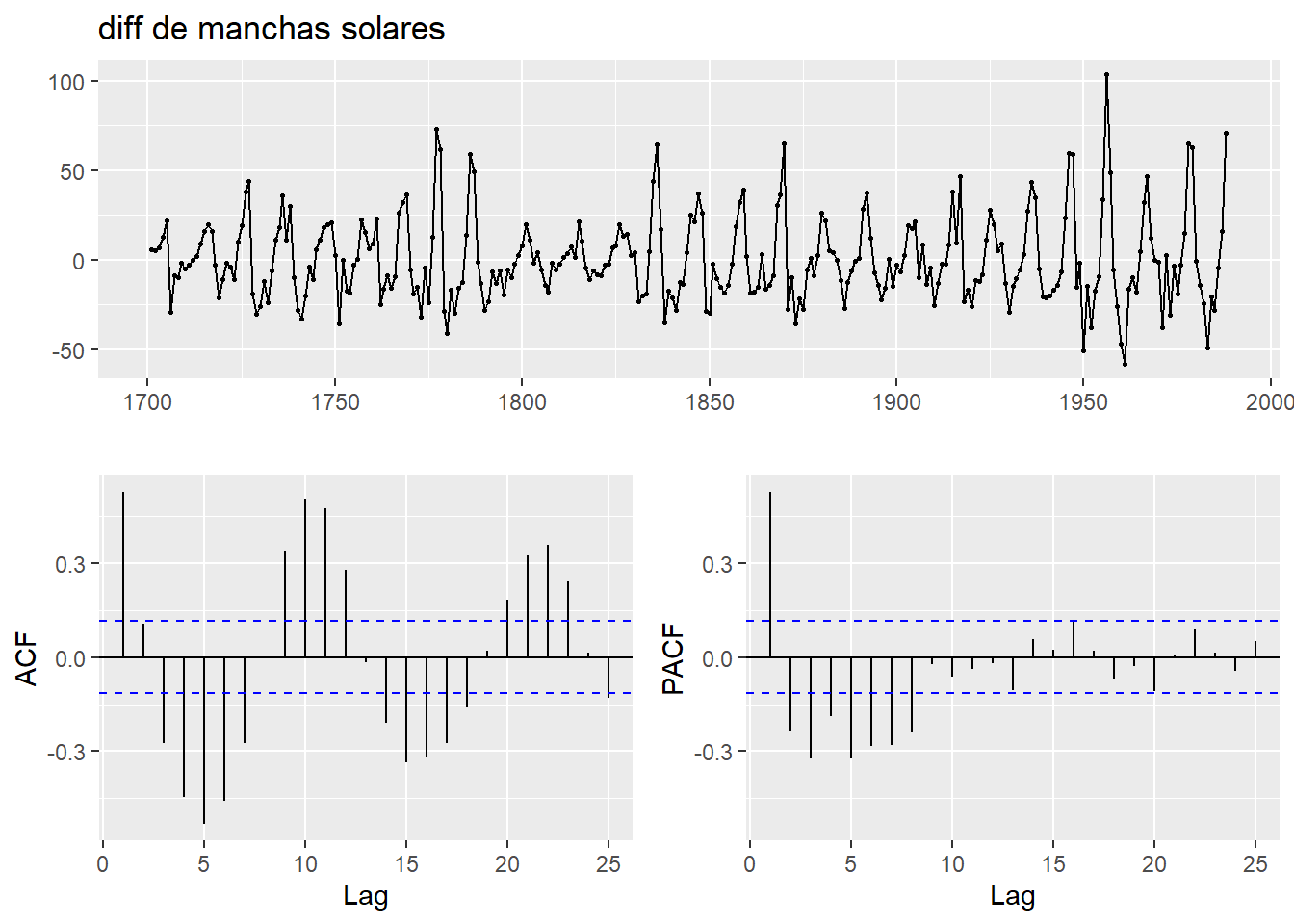 Con esto podemos inferir ya los órdenes del modelo interpretando según la tabla guía:
Con esto podemos inferir ya los órdenes del modelo interpretando según la tabla guía:
- la gráfica sigue mostrando ciclos, aunque de menor magnitud.
- Las ACF tiene cola larga, oscilante + -, con muchos valores significativos, pero un corte tras
lag=1. - La PACF se corta en lag=8.
Con estas observaciones podríamos proponer varios modelos, como un MA(1),un ARIMA(8,1,0) o ARIMA(8,1,1).
Como parece tener ciclos la diff, vamos a pasar un test estadísticos adf. Este test puede servirnos para comprobar que la serie diff(sunspot.year) es estacionaria. El p-valor \(< 0.05\) es indicativo de estacionariedad, un valor mayor es indicativo de serie correlacionada.
library(tseries)
adf.test(diff(sunspot.year), alternative = "stationary")##
## Augmented Dickey-Fuller Test
##
## data: diff(sunspot.year)
## Dickey-Fuller = -14.549, Lag order = 6, p-value = 0.01
## alternative hypothesis: stationaryEl p-valor obtenido es menor de 0,01 < 0,05 por lo que diff(sunspot.year) es estacionaria según el test, aunque no lo parezca.
Vamos a aplicar entonces algunos de los modelos propuestos a mano como ARIMA(8,1,0) con la función sarima() y vemos los resultados del pronóstico. Anoto que seleccionar un orden 8 es una barbaridad, siempre hay que intentar un orden bajo, pero estamos aprendiendo:
# aplico modelo con sarima()
mod<-sarima(sunspot.year,8,1,0)## initial value 3.175447
## iter 2 value 2.956772
## iter 3 value 2.847141
## iter 4 value 2.802982
## iter 5 value 2.757423
## iter 6 value 2.725953
## iter 7 value 2.713005
## iter 8 value 2.712582
## iter 9 value 2.712422
## iter 10 value 2.712412
## iter 11 value 2.712412
## iter 11 value 2.712412
## iter 11 value 2.712412
## final value 2.712412
## converged
## initial value 2.715172
## iter 2 value 2.715157
## iter 3 value 2.715093
## iter 4 value 2.714987
## iter 5 value 2.714963
## iter 6 value 2.714888
## iter 7 value 2.714876
## iter 8 value 2.714875
## iter 9 value 2.714875
## iter 9 value 2.714875
## iter 9 value 2.714875
## final value 2.714875
## converged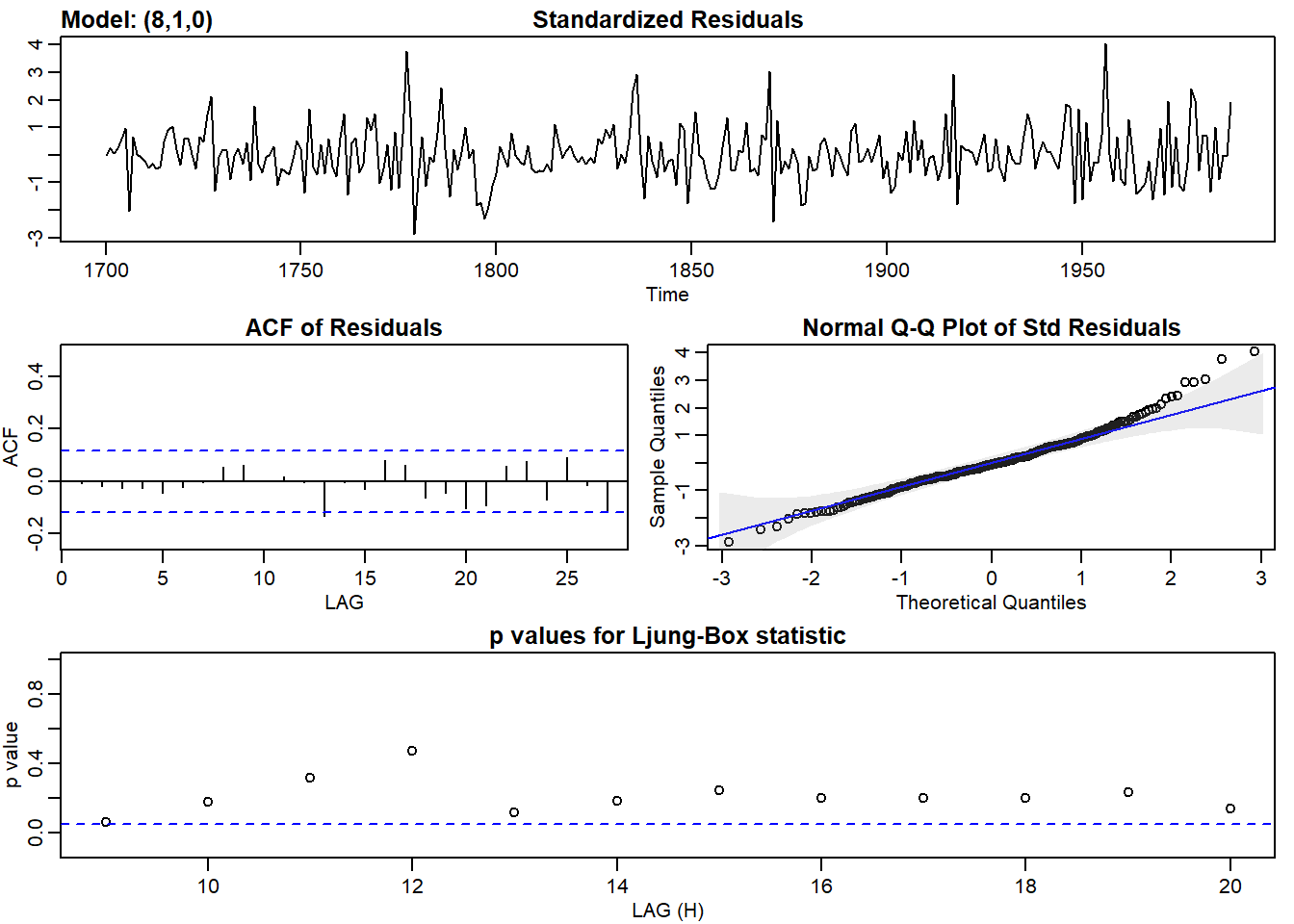
mod$AIC## [1] 8.337071Las 4 gráficas de residuos que muestra sarima() son muy interesantes, la primera es la serie de residuos donde interesa ver su forma, si hay periodos, varianza y amplitud. La segunda es la ACF de los residuos, si no hay valores significativos es que es ruido blanco y el modelo va por buen camino. La terdeca es la Q-Q que muestra como se aproximan los resíduos a una Normal. La ultima de abajo son los p-valores del test de Ljung-Box que indica para cada Lag o retardo si la serie de resiudos tiene o no correlación. Unos valores bajos por debajo de la linea azul es malo, pues indica que los residuos están correlacionados, y que por tant queda información que no ha captado el modelo.
En este caso la solución del modelo parece bastante buena. Si quisieramos hacer un pronóstico es bien fácil usando sarima.for()
# hacemos el pronostico para 10 años
sarima.for(sunspot.year, n.ahead = 12, p = 8, d = 1, q = 0)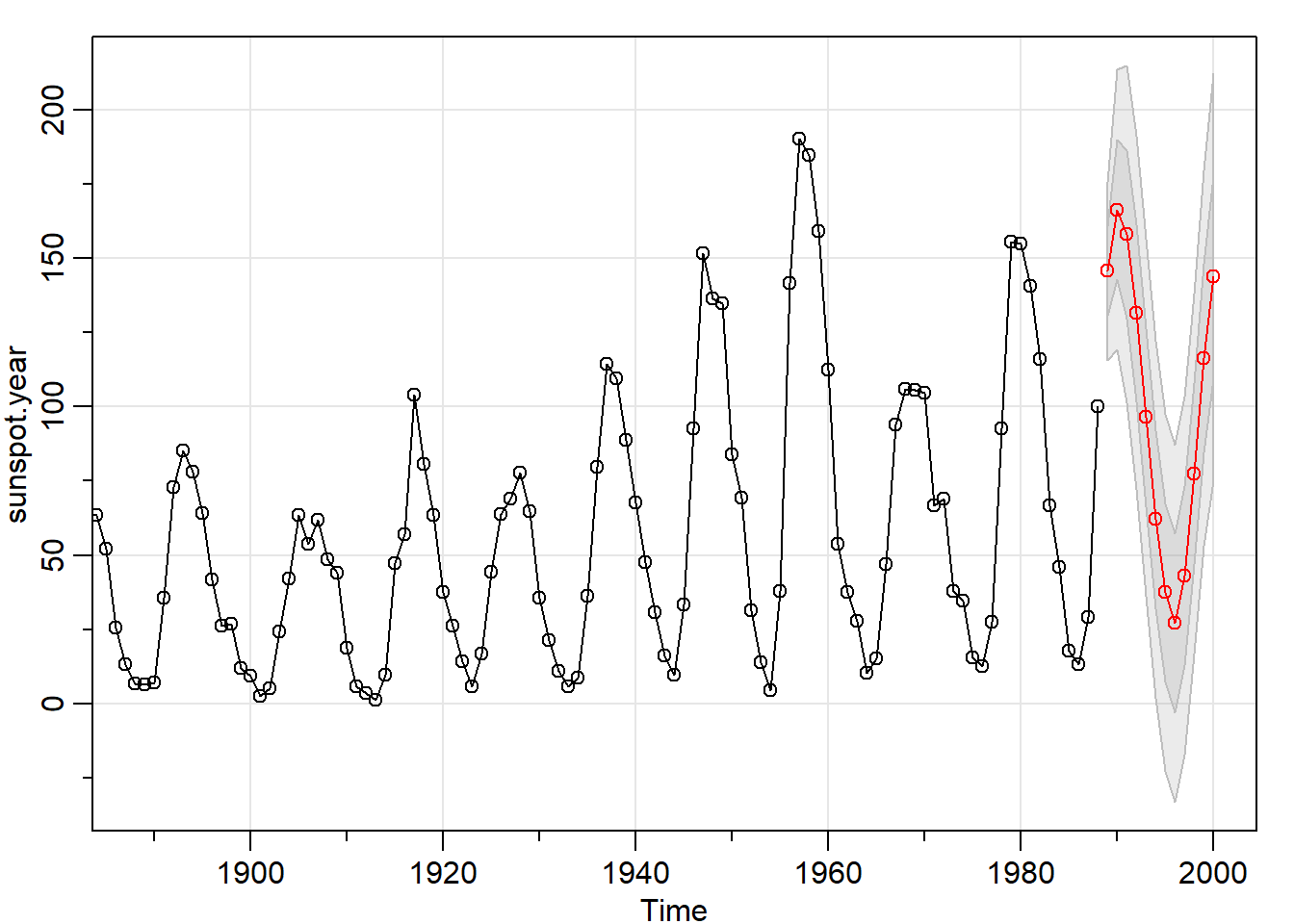
## $pred
## Time Series:
## Start = 1989
## End = 2000
## Frequency = 1
## [1] 145.69750 166.28958 157.97936 131.52315 96.37224 62.03462 37.39309
## [8] 27.07301 43.05197 77.38697 116.28691 143.66324
##
## $se
## Time Series:
## Start = 1989
## End = 2000
## Frequency = 1
## [1] 15.01522 23.56824 28.31877 29.72134 30.04580 30.05569 30.06282 30.07081
## [9] 30.07150 30.30438 31.61150 34.21189Ahora que hemos hecho lo dificil, vamos a ver cómo ir directos al grano con la función de forecast auto.arima. esta función ajusta un modelo a los datos así de fácil:
# obtencion automática del modelo de ajuste
auto.arima(sunspot.year)## Series: sunspot.year
## ARIMA(2,1,3)
##
## Coefficients:
## ar1 ar2 ma1 ma2 ma3
## 1.6135 -0.9346 -1.4216 0.4267 0.1373
## s.e. 0.0258 0.0246 0.0617 0.0983 0.0557
##
## sigma^2 estimated as 240.4: log likelihood=-1197.1
## AIC=2406.2 AICc=2406.5 BIC=2428.17El resultado es un modelo arima(2,1,3). Hay que tener en cuenta que auto.arima tiene algunos parámetros por defecto como que el orden sea menor de 5. Si queremos que trabaje duro podemos indicar stepwise = TRUE para ver si obtiene otro modelo mejor.
mod_auto<-sarima(sunspot.year,2,1,3)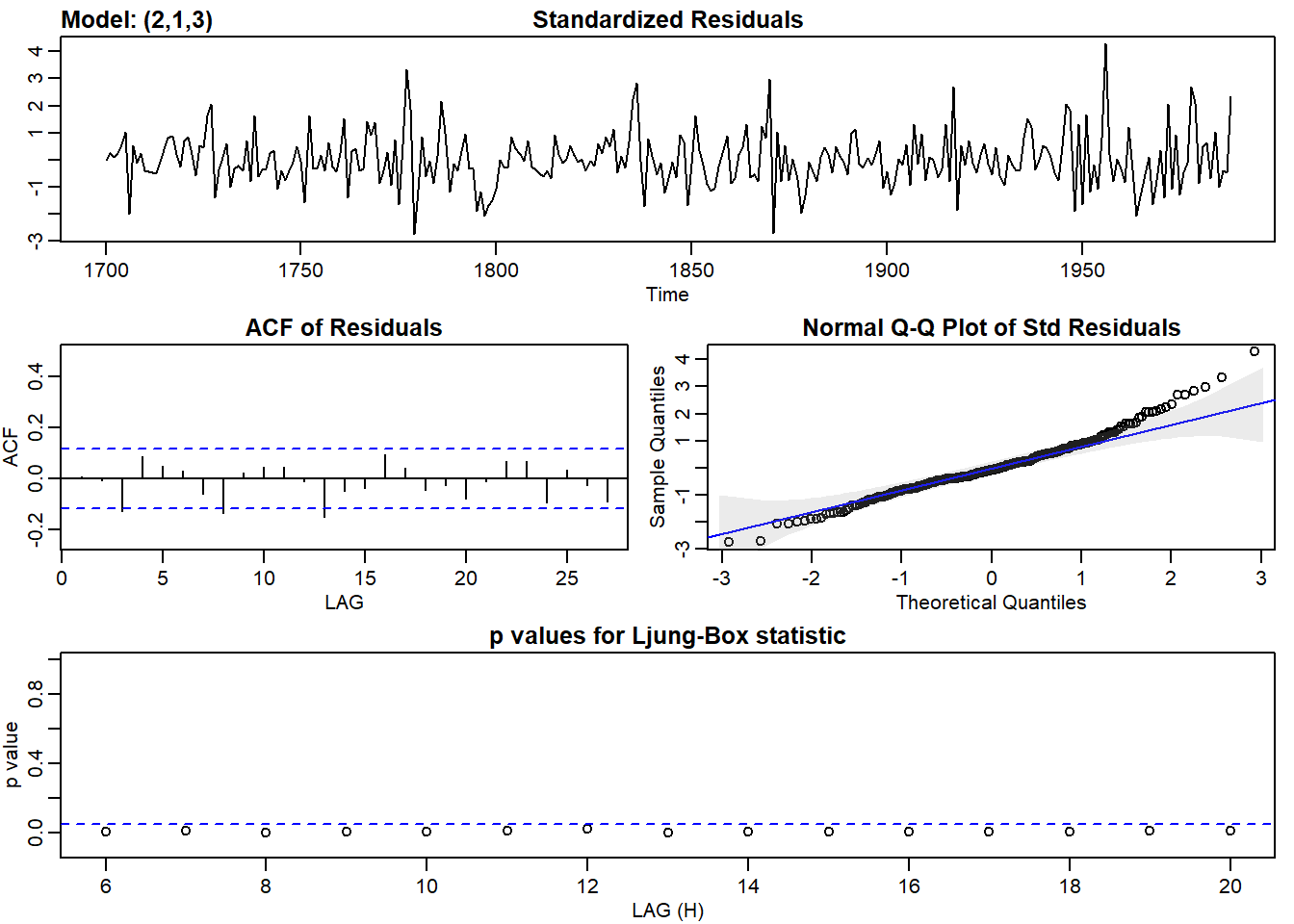 Para comparar diferentes modelos podemos usar alguno de los indicadores AIC, AICc o BIC, el modelo con menor valor es el mejor.
Para comparar diferentes modelos podemos usar alguno de los indicadores AIC, AICc o BIC, el modelo con menor valor es el mejor.
print(paste("modelo arima(2,1,3)AIC=",round(mod_auto$AIC,2),"modelo arima(8,1,0)AIC=", round(mod$AIC,2)))## [1] "modelo arima(2,1,3)AIC= 8.36 modelo arima(8,1,0)AIC= 8.34"Aunque los resultados son parecidos tiene mejor ajuste el modelo que hemos deducido nosotros arima(8,1,0) que el que obtiene la función auto.arima, ya que el AIC es menor.
Ejemplo 2. AirPassengers.
Ahora vamos a ajustar un modelo arima y hacer un pronostico a la serie temporal AirPassengers. Esta serie está incluida en el dataset de R y almacena los datos mensuales de pasajeros aéreos de vuelos internacionales entre 1940 y 1960.
Vamos a inciar con los mismos pasos, pintar las graficas de la serie y ACF y PACF, despues calculamos las diff que ndiff, y vemos qué pasa:
library(forecast)
library(ggplot2)
library(xts)
# vamos a ver de qué años es la serie:
periodicity(AirPassengers)## Monthly periodicity from ene. 1949 to dic. 1960# pintamos la gráficas ACF..
ggtsdisplay(AirPassengers)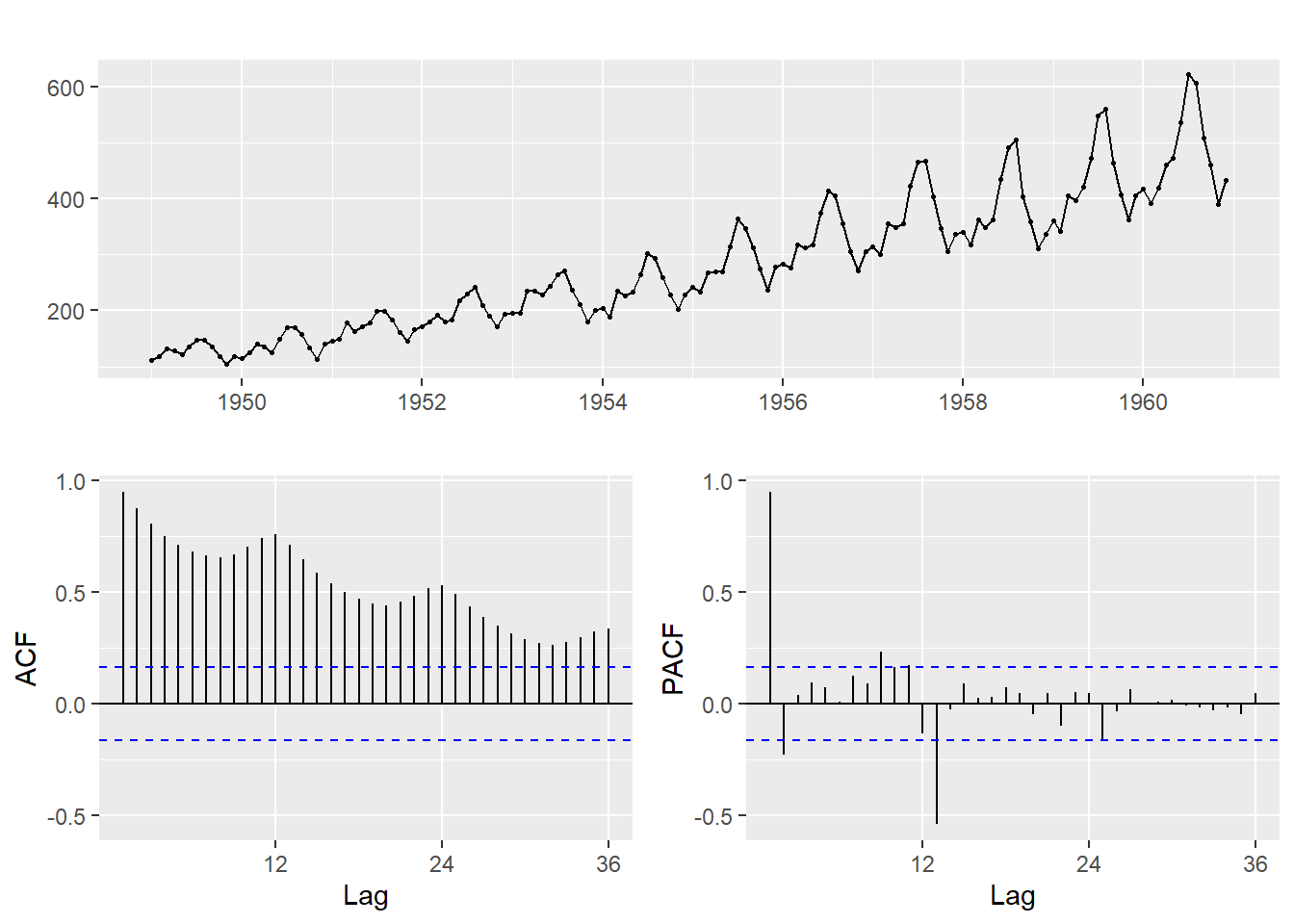
# caluclamos las diferencias básicas y estacionales
ndiffs(AirPassengers)## [1] 1nsdiffs(AirPassengers)## [1] 1La serie parece que no tiene valores fuera de rango ni ausentes.
Los resultados de las funciones ndiffs nos indican que la serie necesita diferenciarse para ser estacionaria, y que tiene un ciclos periódicos o estacionales, lo que nos lleva a la complicación de usar el modelo general de arima(p,d,q)(P,D,Q)S con 3 órdenes más.
También observamos que tiene tendencia alcista y varianza no homogenea, con claro aumento de la amplitud de los ciclos con el tiempo.
Transformación para homogeneizar varianza
La tendencia se quita al diferenciar la serie original una vez, pero la varianza no se va con la diferenciación. Se debe hacer una transformación adicional tomando logaritmos o usando la forma generalizada de la función Box-Cox, que necesita un solo parámetro lambda.
Usaremos esta última opción que es más generalista:
# calculamos el valor de lambda
lambda <- BoxCox.lambda(AirPassengers)
# La serie transformada, homogenea en varianza es esta:
air_t<-BoxCox(AirPassengers,lambda)
# pintamos a efectos de ver la reducción de varianza
plot(cbind(AirPassengers,air_t), main="Comparativa serie origen y transformada Box-Cox")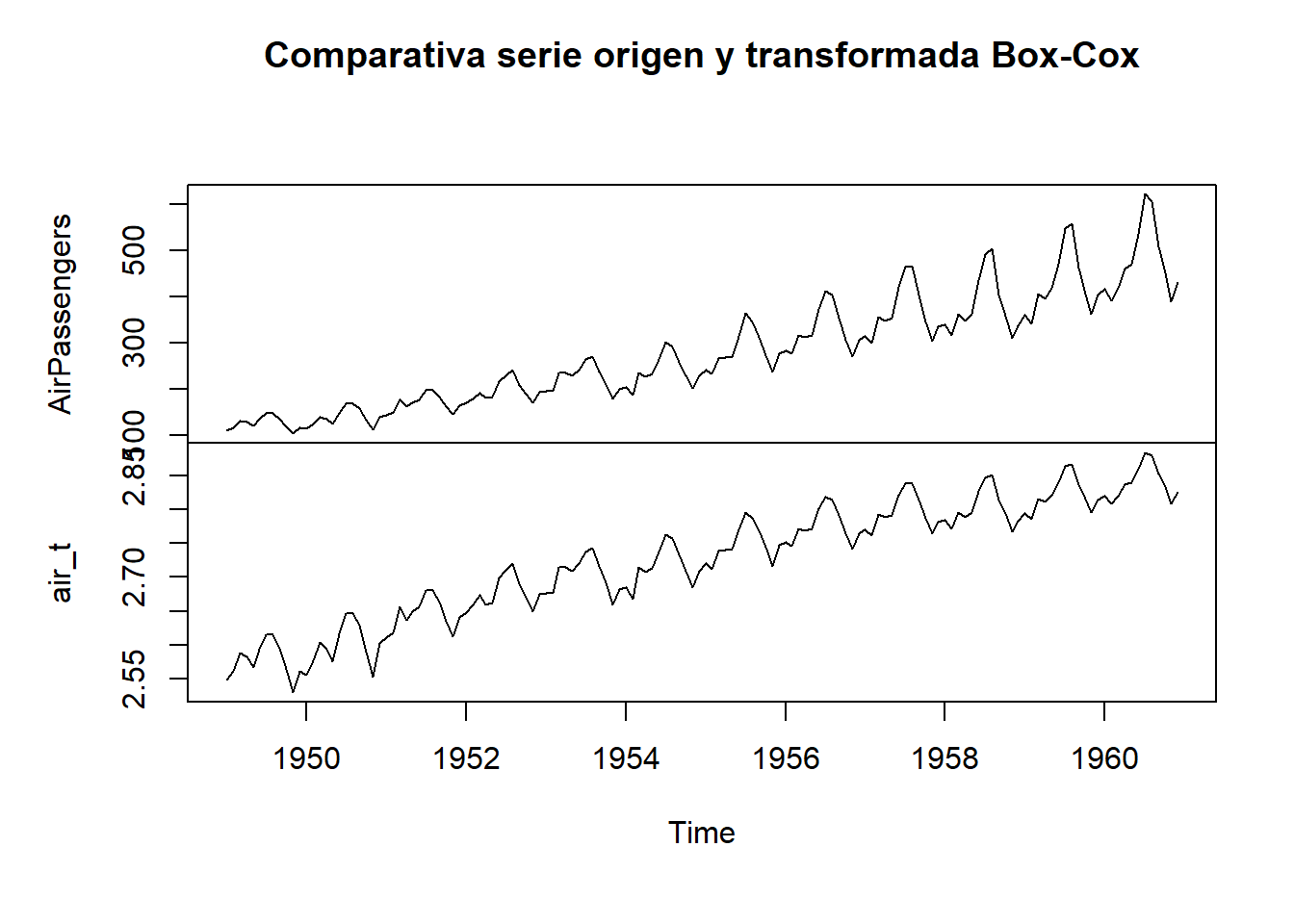 Como vemos la transformada tiene una amplitud de ciclos más homogénea. Usaremos esta transformada para diferenciarla y obtener una serie estacionaria sobre la que aplicar el modelo arima.
Como vemos la transformada tiene una amplitud de ciclos más homogénea. Usaremos esta transformada para diferenciarla y obtener una serie estacionaria sobre la que aplicar el modelo arima.
# diferenciamos una vez como nos indicó ndiffs
air_td1<-diff(air_t)
ggtsdisplay(air_td1) # =tsdisplay(air_td1)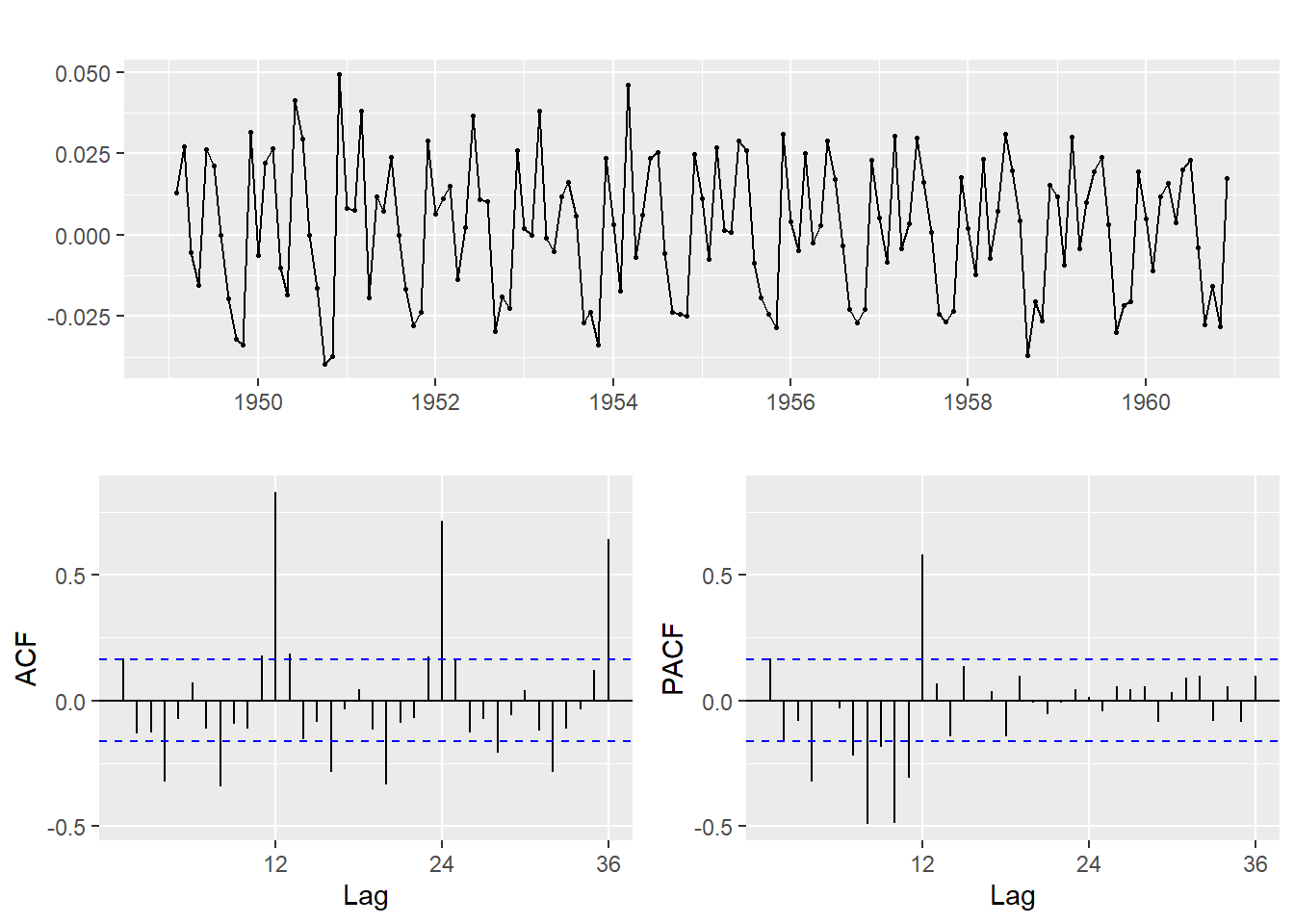
acf2(air_td1) # lo pintamos mejor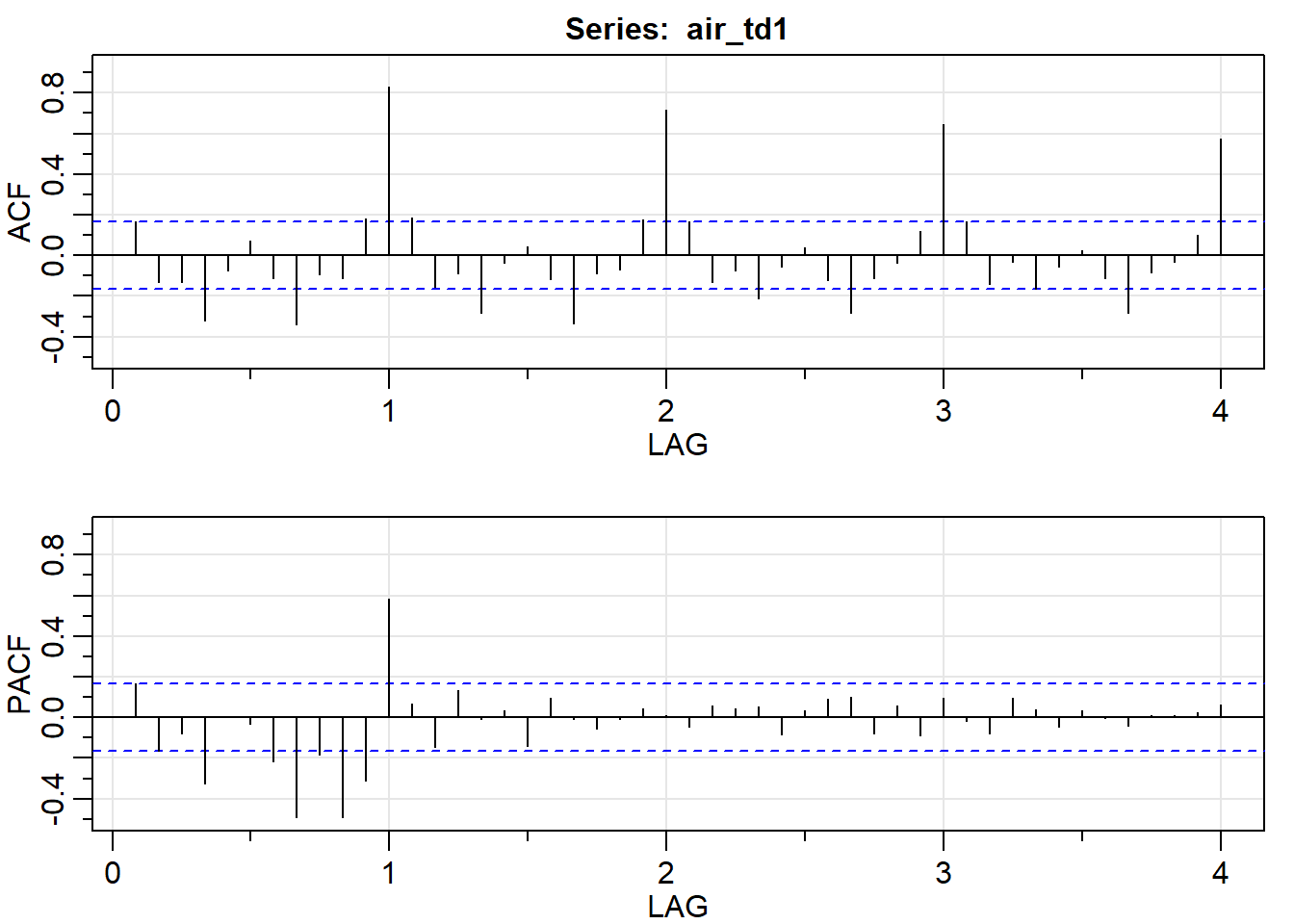
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## ACF 0.17 -0.13 -0.13 -0.32 -0.07 0.07 -0.11 -0.34 -0.10 -0.11 0.18 0.83
## PACF 0.17 -0.17 -0.08 -0.33 0.00 -0.03 -0.22 -0.49 -0.19 -0.49 -0.31 0.58
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
## ACF 0.19 -0.16 -0.09 -0.28 -0.04 0.05 -0.12 -0.33 -0.09 -0.07 0.17 0.72
## PACF 0.07 -0.14 0.14 -0.01 0.04 -0.14 0.10 -0.01 -0.06 -0.01 0.04 0.01
## [,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36]
## ACF 0.17 -0.13 -0.07 -0.21 -0.06 0.04 -0.12 -0.28 -0.11 -0.04 0.12 0.64
## PACF -0.04 0.06 0.05 0.05 -0.08 0.03 0.09 0.10 -0.08 0.06 -0.09 0.10
## [,37] [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
## ACF 0.17 -0.14 -0.03 -0.16 -0.06 0.02 -0.11 -0.28 -0.09 -0.03 0.10 0.58
## PACF -0.02 -0.08 0.10 0.04 -0.05 0.04 0.00 -0.04 0.01 0.01 0.03 0.06Las gráficas ACF y PACF de la serie air_td1 muestran picos claros cada rezago lag=12, es decir ciclos anuales, ya que la serie es mensual. Será este el ciclo que nos indicaba ndiffs, por lo que tenemos identificado el periodo S=12.
Aparte la ACF tiene solo el primer valor significativo y por poco, en la PACF son los dos primeros los que son significativos. Esto nos puede indicar un ARMA(2,1) que con el I(1) sería un arima(2,1,1)
Para los ordenes del ciclo pintamos la serie diff(,lag=12) y buscaremos allí los órdenes (P,D,Q).
# Diferenciamos la serie lag=12 para ver estacionalidad
#air_td12<-diff(air_td1,lag=12)
air_t12<-diff(air_t,lag=12)
ndiffs(air_t12)## [1] 1La serie debe diferenciarse, según nos muestra ndiffs. Lo hacemos sabiendo ya que I(D=1)12.
tsdisplay(diff(air_t12))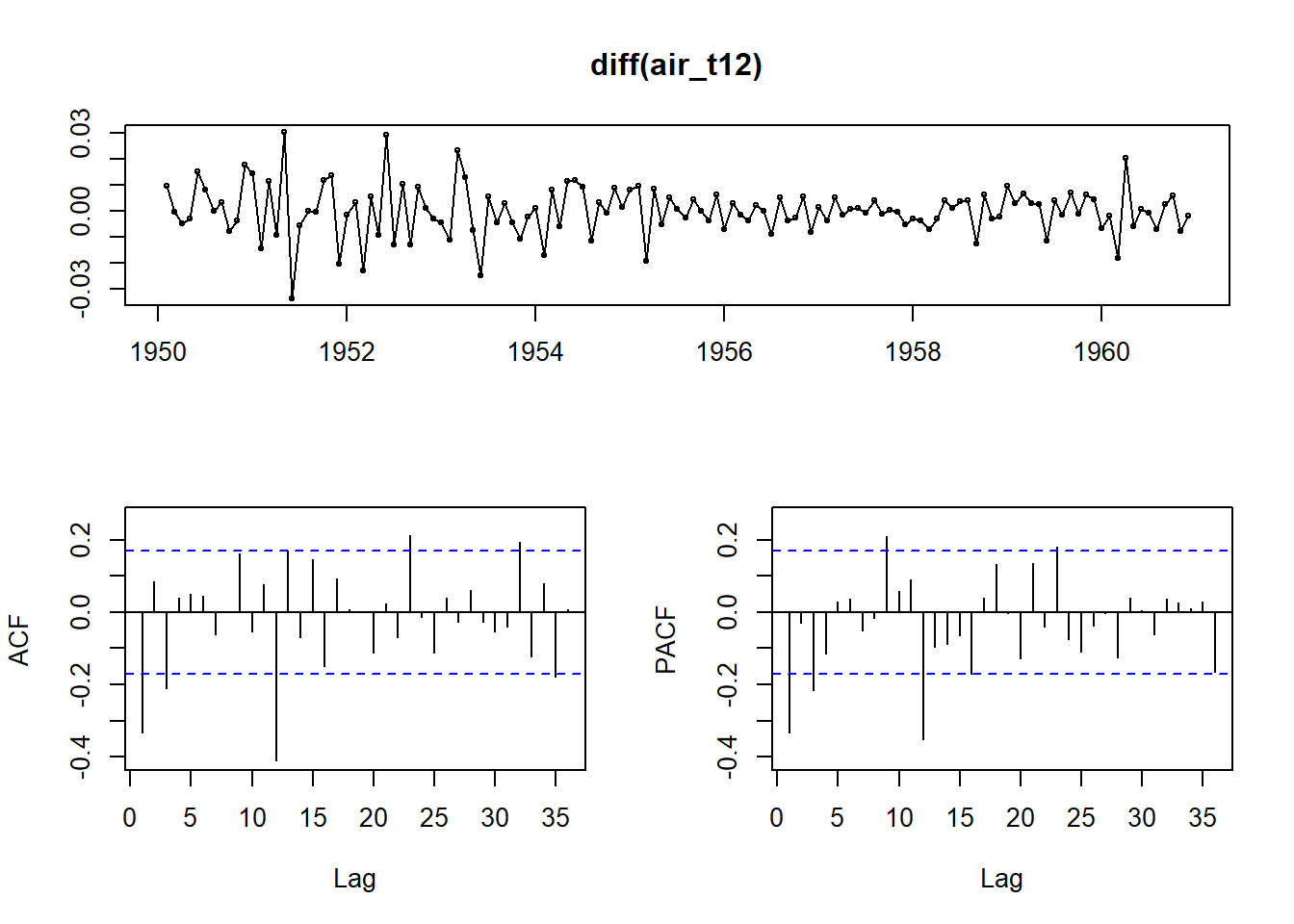 La serie estacional diferenciada muestra en la ACF el primer valor significativo y el siguiente cero e igual en la PACF, tendríamos un
La serie estacional diferenciada muestra en la ACF el primer valor significativo y el siguiente cero e igual en la PACF, tendríamos un arima(1,1,1)12 para la serie estacional.
En definitiva podríamos concluir que una primera aproximación podría ser un arima(2,1,1)(1,1,1). Con estos supuestos hacemos el pronóstico usando las funciones de la librería astsa:
pronos<-sarima.for(air_td1, n.ahead = 24, p = 2, d = 1, q = 1,P=1,D=1,Q=1,S =12)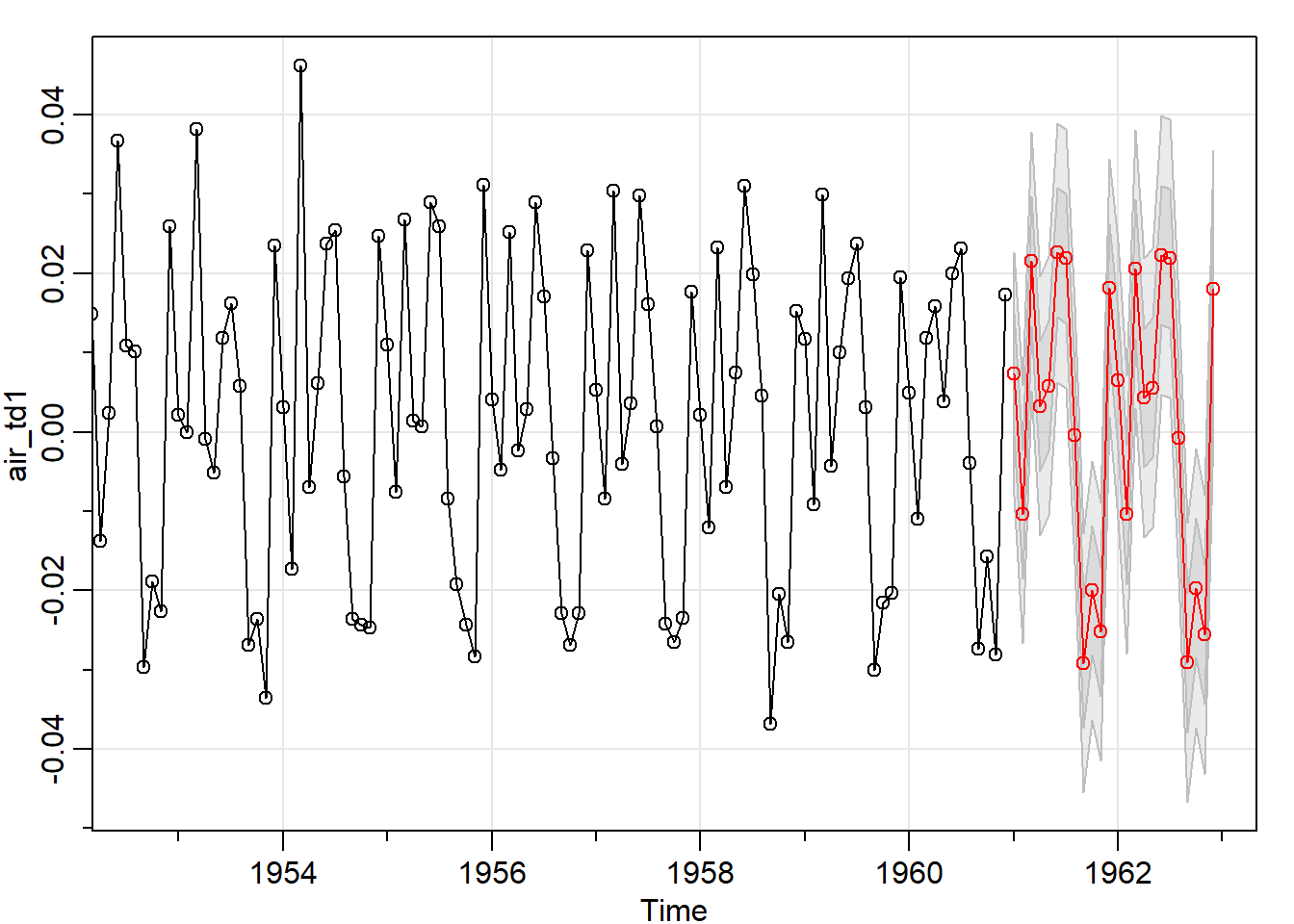 Como vemos el pronóstico se realiza sobre la serie de diferencias transformada, es decir, la serie estacionaria sobre la que aplicamos arima
Como vemos el pronóstico se realiza sobre la serie de diferencias transformada, es decir, la serie estacionaria sobre la que aplicamos arima air_td1 en nuestro caso. Para comparar con la original hay que realizar la trasnformación inversa, como veremos a continuación:
# Pronostico sobre la serie real, tenemos que invertir la transformada asi:
# AirPassengers-->boxcox-->air_t-->diff-->air_td1
# ahora hacemos el inverso y lo dibujamos junto a la original:
autoplot(AirPassengers)+
autolayer(InvBoxCox(diffinv(pronos$pred,xi=last(air_t)), lambda))+
theme(legend.position = "none") 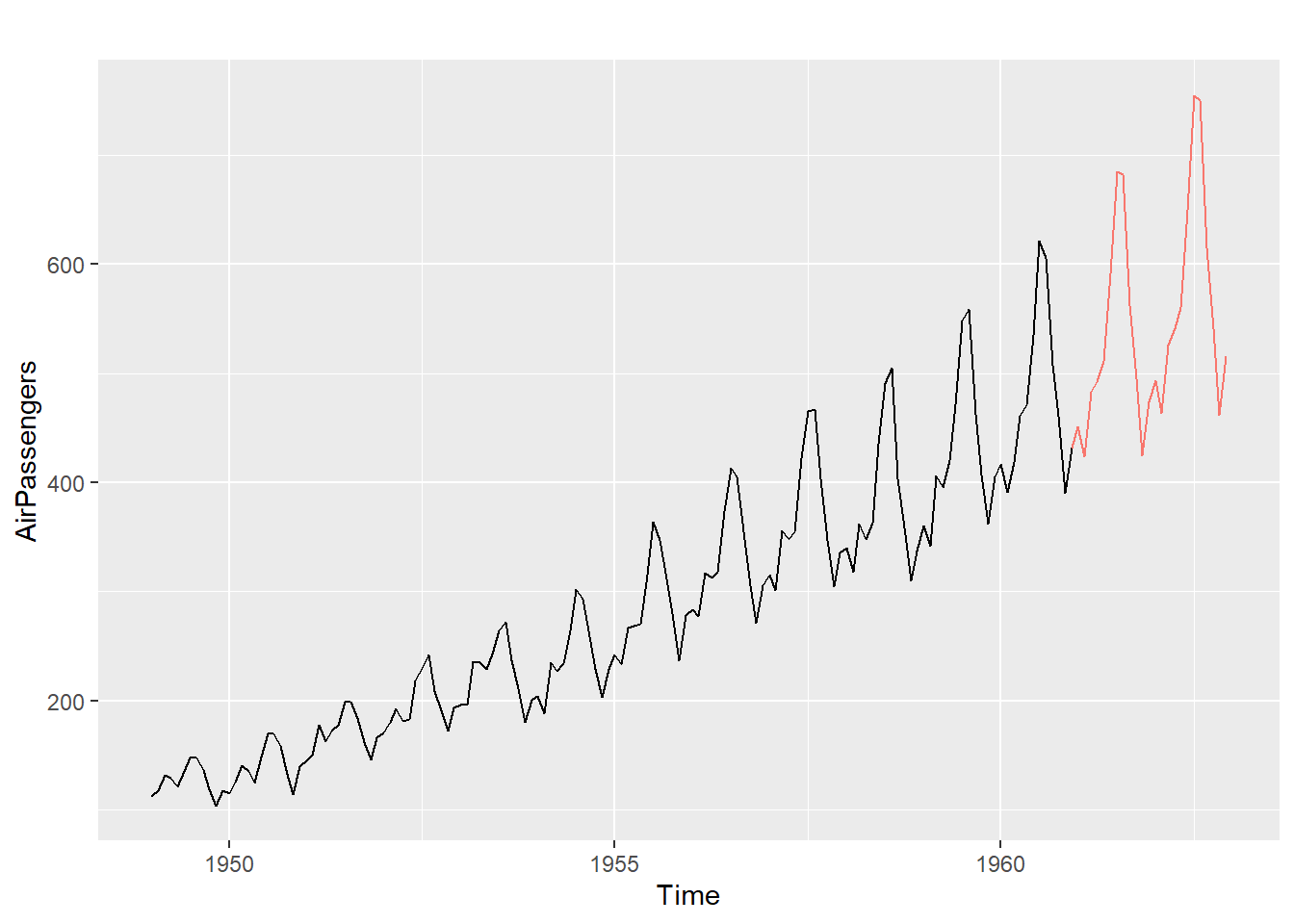
Usando forecast
Vamos a hacer el modelo de la misma serie, pero usando el paquete forecast, que simplifica la tarea con sus funciones.
Lo primero es sacar un ajuste automático con la función auto.arima. El resultado lo almacenamos en la variable fit, que contiene los parámetros del modelo arima.
El pronóstico se realiza simplemente usando la función forecast(modelo, h=..).
fit <- auto.arima(AirPassengers, seasonal=T)#,lambda="auto")
checkresiduals(fit)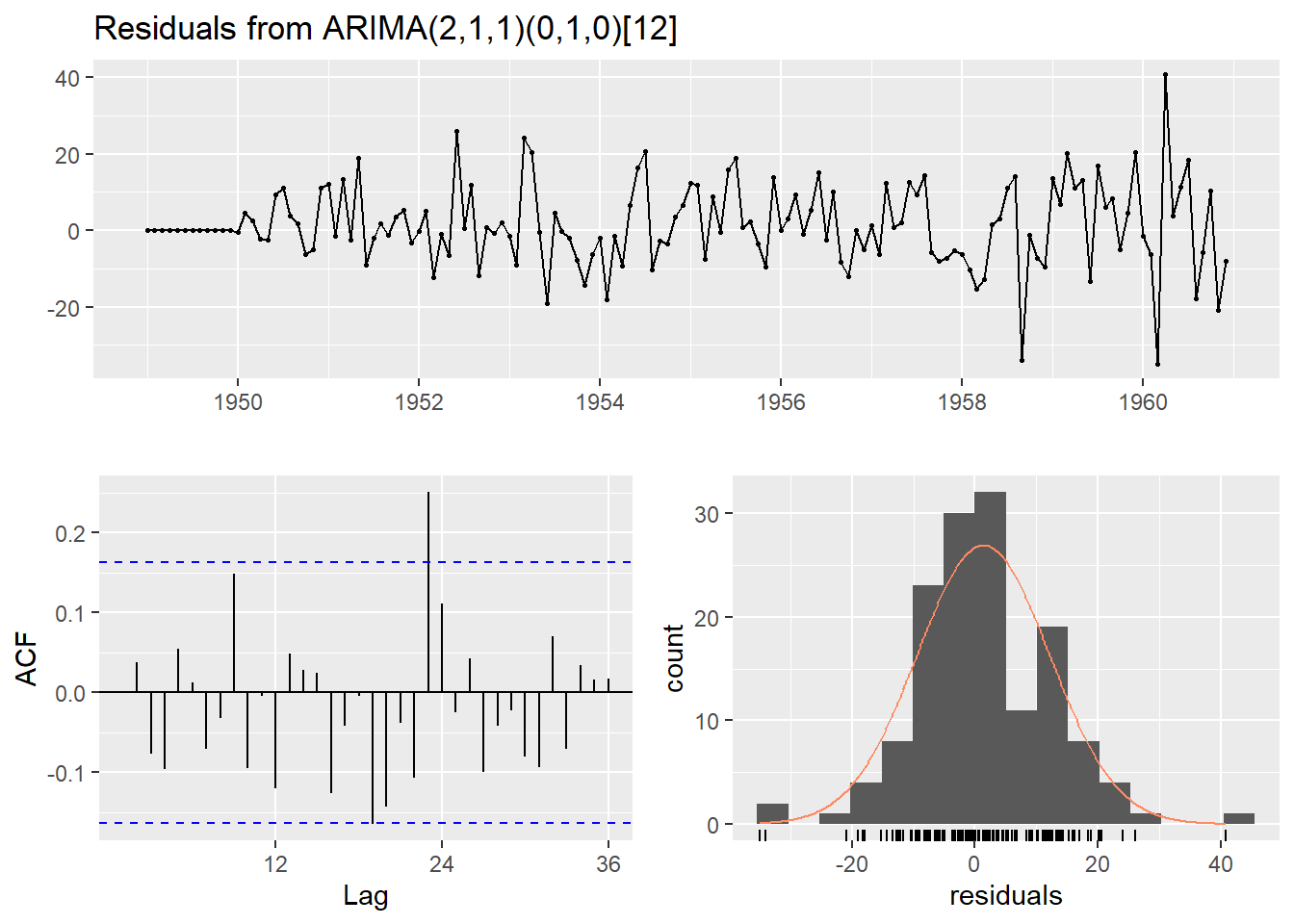
##
## Ljung-Box test
##
## data: Residuals from ARIMA(2,1,1)(0,1,0)[12]
## Q* = 37.784, df = 21, p-value = 0.01366
##
## Model df: 3. Total lags used: 24plot(forecast(fit))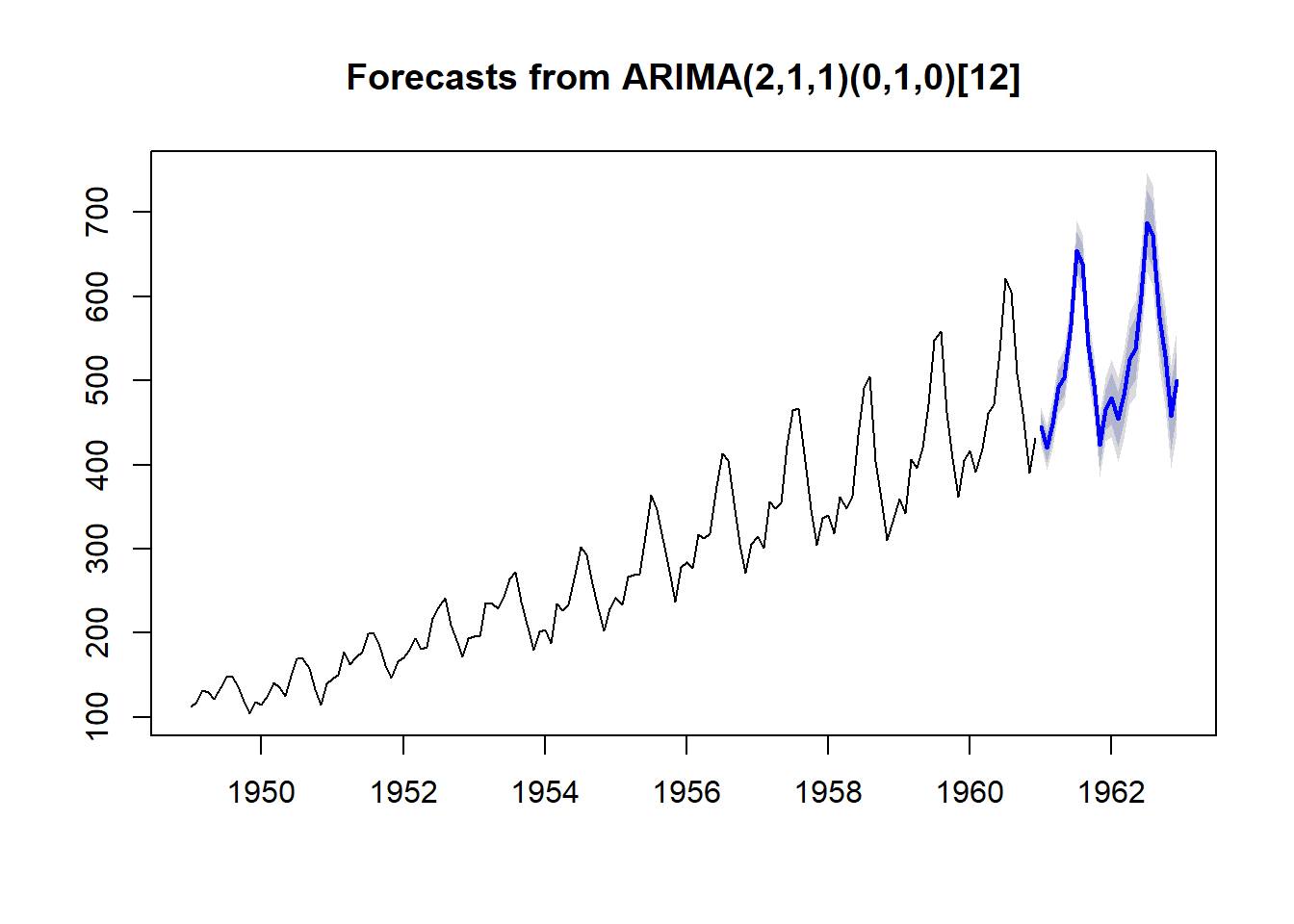 El modelo auto nos da unos órdenes
El modelo auto nos da unos órdenes ARIMA(2,1,1)(0,1,0)[12], pero si comprobamos los residuos vemos que no cumplen el criterio de ser ruido blanco, al tener un p-valor menor de 0,05. Esto es porque olvidamos un punto importante y es que no hemos fijado lambda y por defecto este valor es nulo, lo que equivale a no hacer ninguna transformacion de varianza. Dejamos la forma buena de llamar a la función en comentario, aunque no la desarrollemos más.
Si quisieramos comprobar el pronostico actual con el modelo anterior arima(2,1,1)(1,1,1)12 lo haríamos así: primero creamos el modelo en formato forecast y después pintamos ambos juntos.
#`arima(2,1,1)(1,1,1)`
air.fit <- Arima(AirPassengers, order=c(2,1,1), seasonal=list(order=c(1,1,1),period=12)
,lambda=lambda)
checkresiduals(air.fit)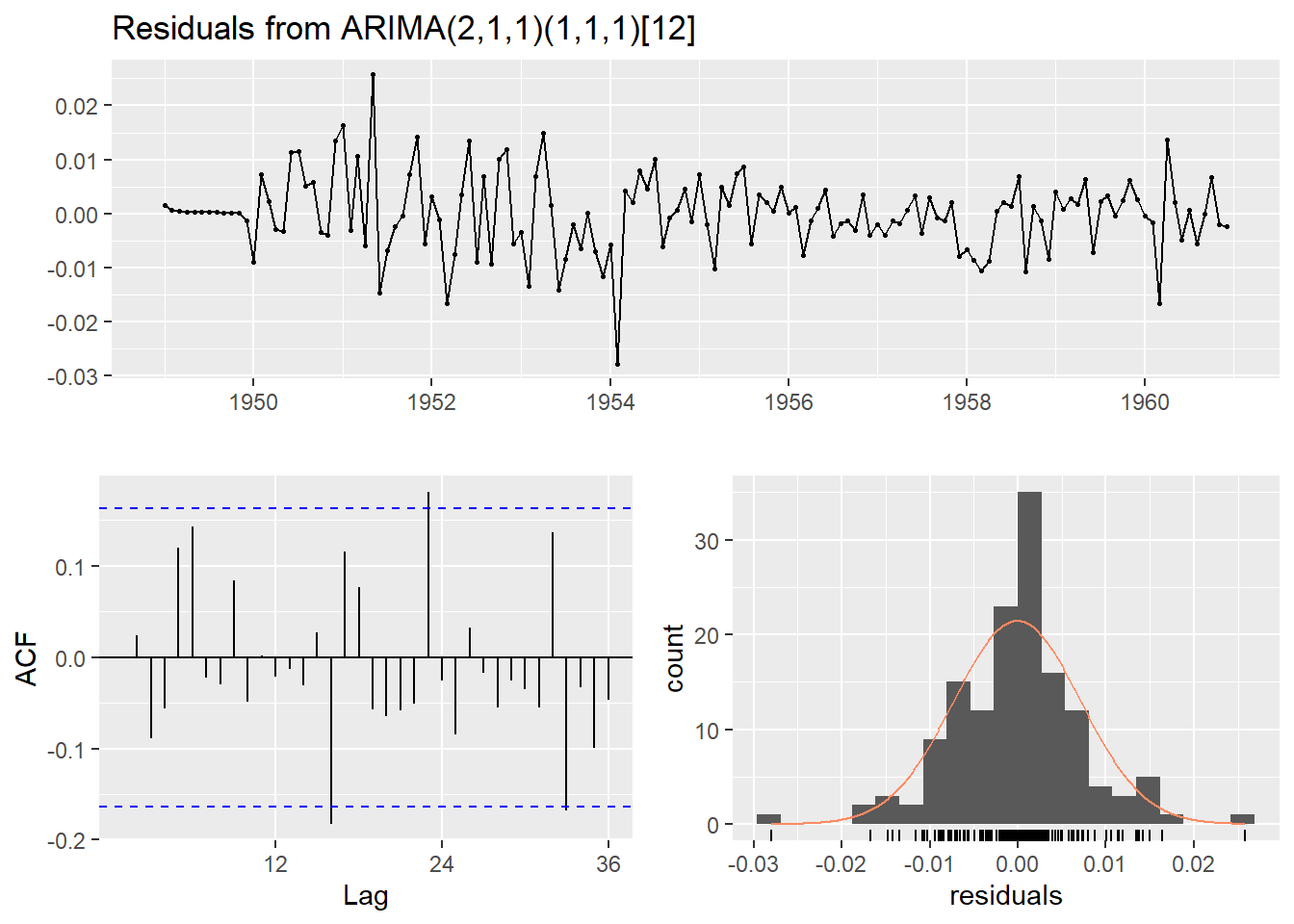
##
## Ljung-Box test
##
## data: Residuals from ARIMA(2,1,1)(1,1,1)[12]
## Q* = 25.865, df = 19, p-value = 0.134
##
## Model df: 5. Total lags used: 24plot(forecast(air.fit))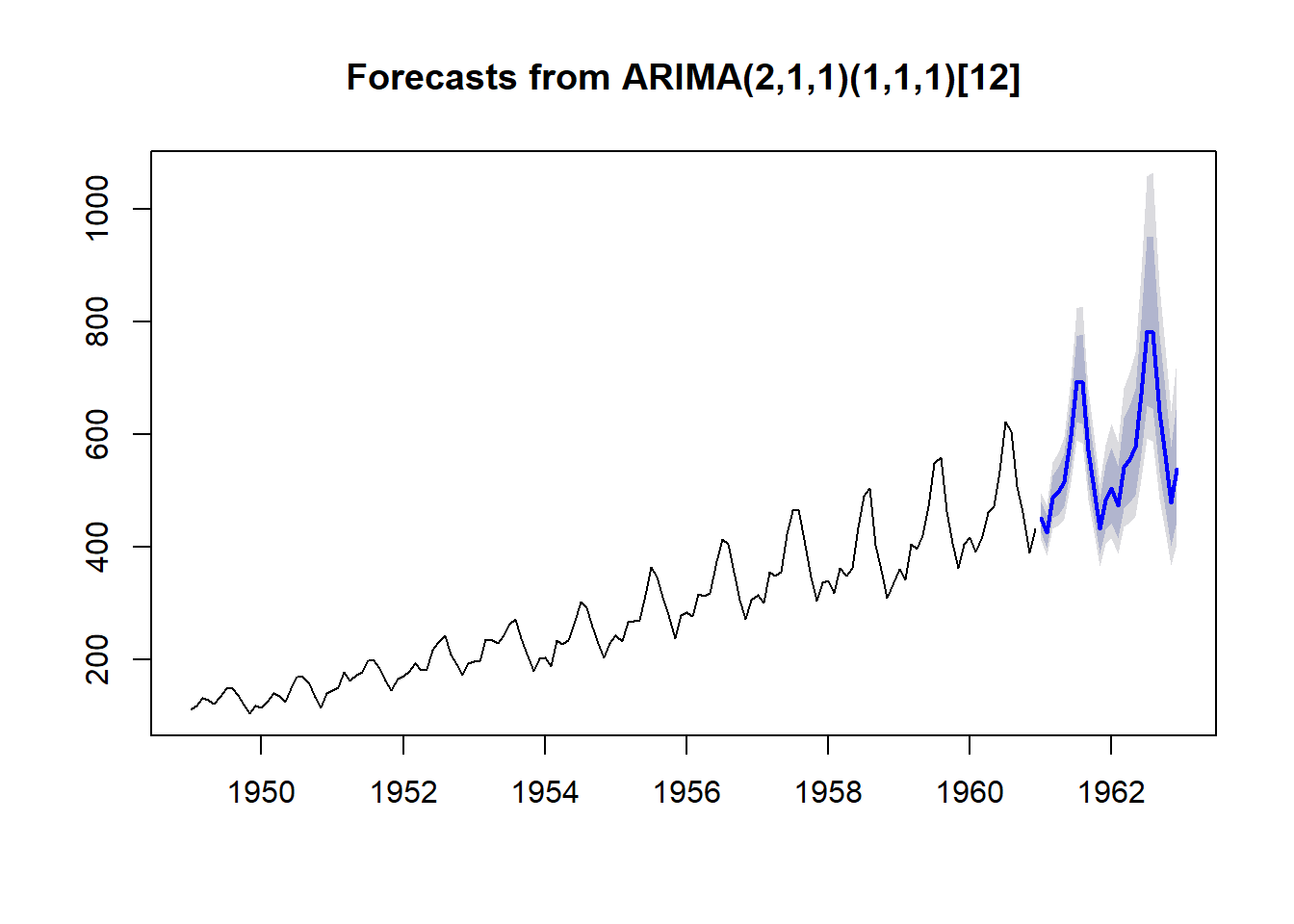 Comparamos ambos modelos, el automático y el que hemos deducido de las gráficas a ojo, y veremos que los pronósticos son diferentes:
Comparamos ambos modelos, el automático y el que hemos deducido de las gráficas a ojo, y veremos que los pronósticos son diferentes:
# hacemos un pronostico a 3 años con cada modelo
pronos01<-forecast(fit,h=36)
pronos02<-forecast(air.fit,h=36)
#pronos01$mean
#pronos02$mean
# pronos01$mean continene los datos de forecast
# pintamos los pronósticos y la serie, pero para que se vea mejor
# hacemos zoom a una ventana más pequeña desde 1955
autoplot(window(AirPassengers, start =c(1955,1)))+
ylab("pasajeros")+ ggtitle("Pronósticos a 3 años")+
#añadimos pronostico automatico
autolayer(pronos01,PI=F, col="blue",lty=2)+
# añadimos pronos nuestro en rojo
autolayer(pronos02,PI=F, col="red")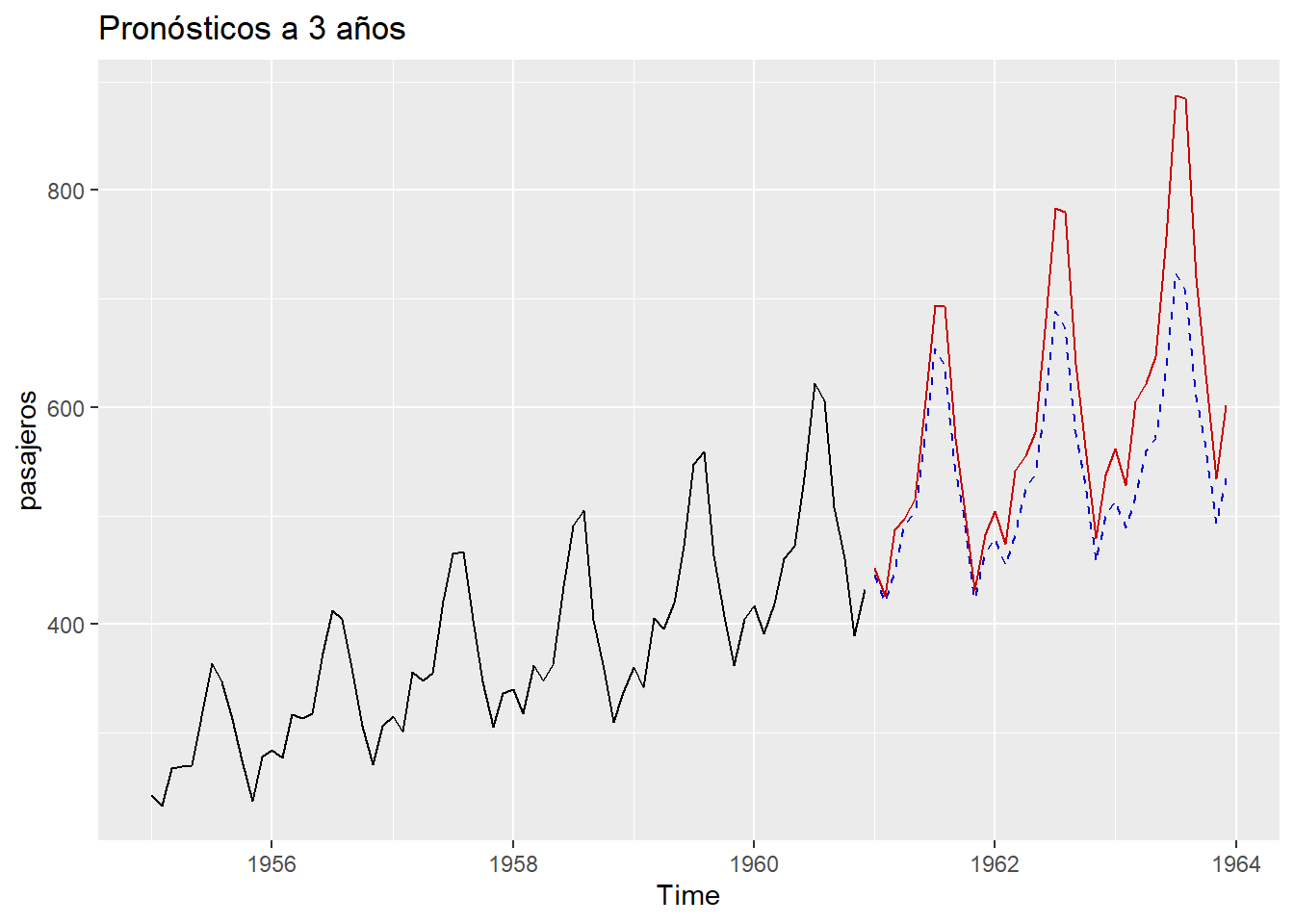
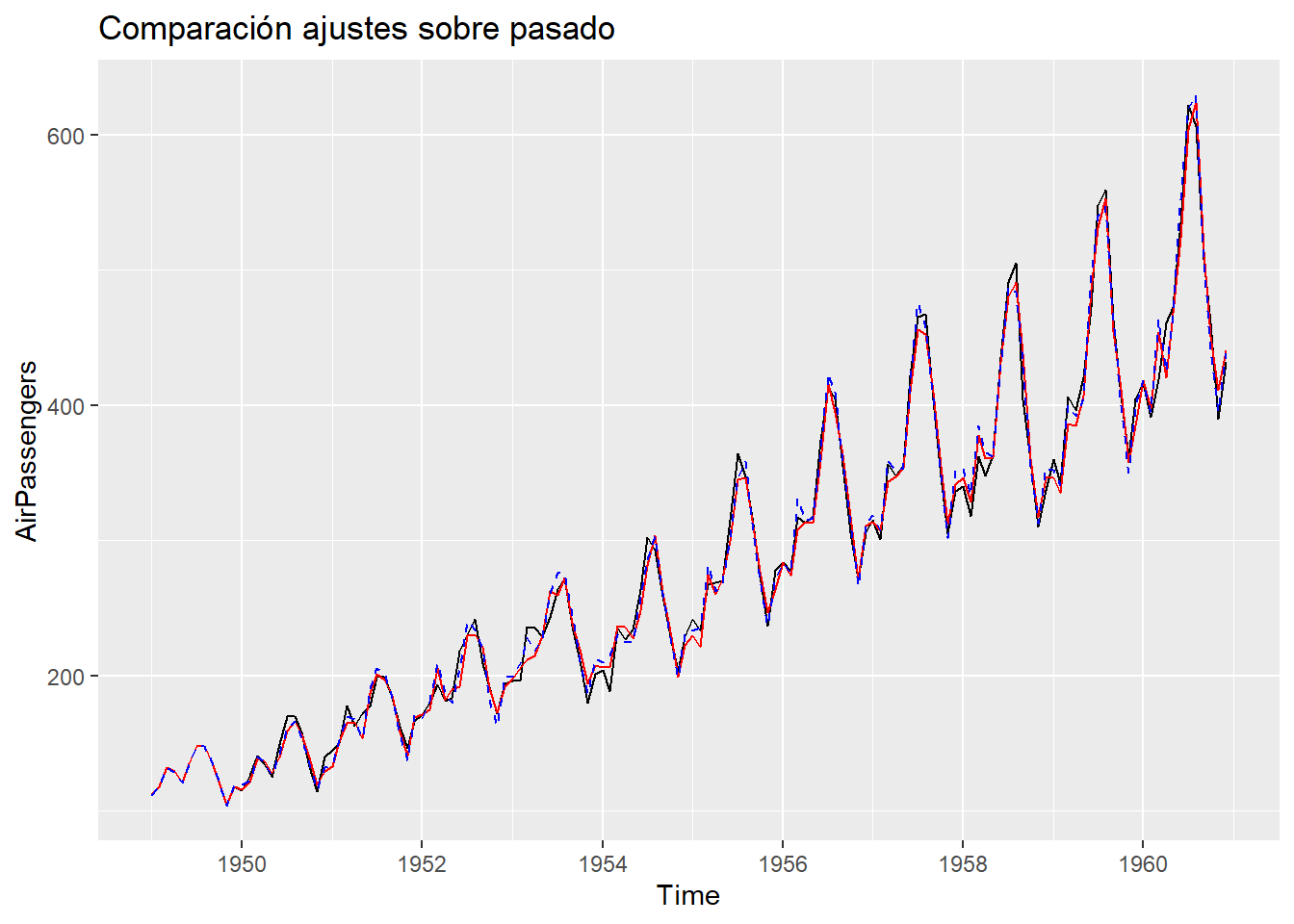
#Comparamos ahora el ajuste en datos pasados
autoplot(AirPassengers) + ggtitle("Comparación ajustes sobre pasado")+
geom_line(
aes(x=time(pronos01$fitted),
y=pronos01$fitted,color="red"),
col = "red"
)+
geom_line(
aes(x=time(pronos02$fitted),
y=pronos02$fitted,color="blue"),
col = "blue", lty=2
)
Ejemplo3. globaltem
Vamos con una serie física globtemp que viene de ejemplo en el paquete astsa. Se trata de una serie temporal anual con datos de las desviaciones sobre la temperatura media en la tierra (calculada de 1951-1980) desde el año 1880 hasta el 2015.
Como siempre, lo primero es ver la serie y autocorrelaciones y calcular ndiffs().
ggtsdisplay(globtemp)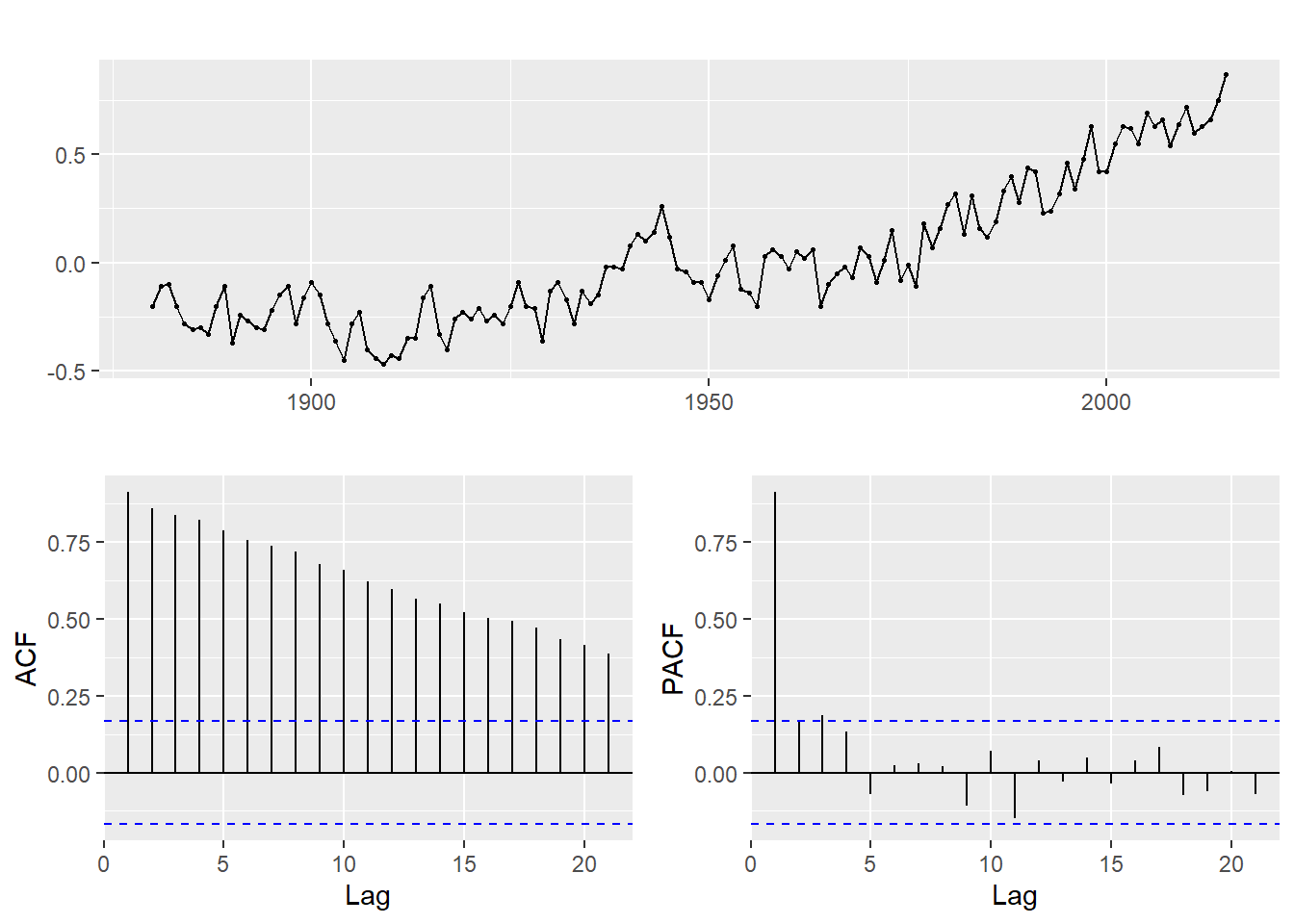
# caluclamos las diferencias básicas y estacionales
ndiffs(globtemp)## [1] 1#nsdiffs(globtemp)De ver las gráficas sacamos:
- La serie tiene tendencia,por lo que habrá que diferenciar.
- no se aprecia cambio significativo de la varianza, por lo que no es necesario hacer transformaciones de varianza.
- el resultado de la función
ndiffs()es uno (1) lo que confirma la diferenciación, y estima I(d=1) o ARIMA(0,1,0)
Vamos con la serie diferenciada.
ggtsdisplay(diff(globtemp),main=" diff globtemp")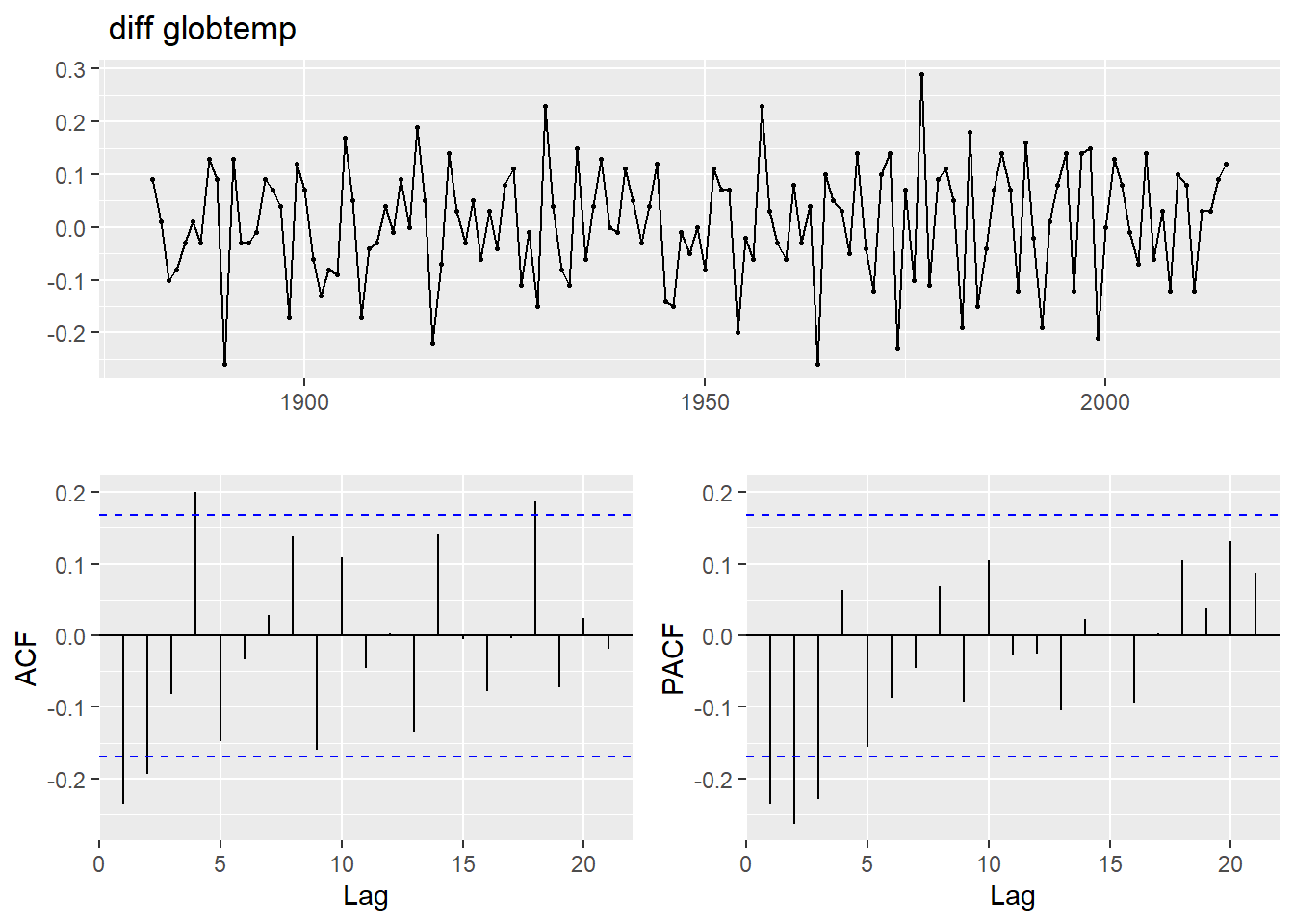 Conclusiones de ver las gráficas:
Conclusiones de ver las gráficas:
- la ACF se corta a partir del lag=2, y la PACF a partir del 3, por lo que podría ser un ARIMA(3,1,2).
- en el lag=4 y 18 hay un pico significativo en ACF lo que podría indicar algún ciclo, aunque no se refleja en el
nsdiffs()como significativo por lo que lo descartamos de momento.
Vamos a ver cómo se comporta el modelo que hemos deducido:
# modelo hecho a ojo
modelo1<-sarima(globtemp,3,1,2)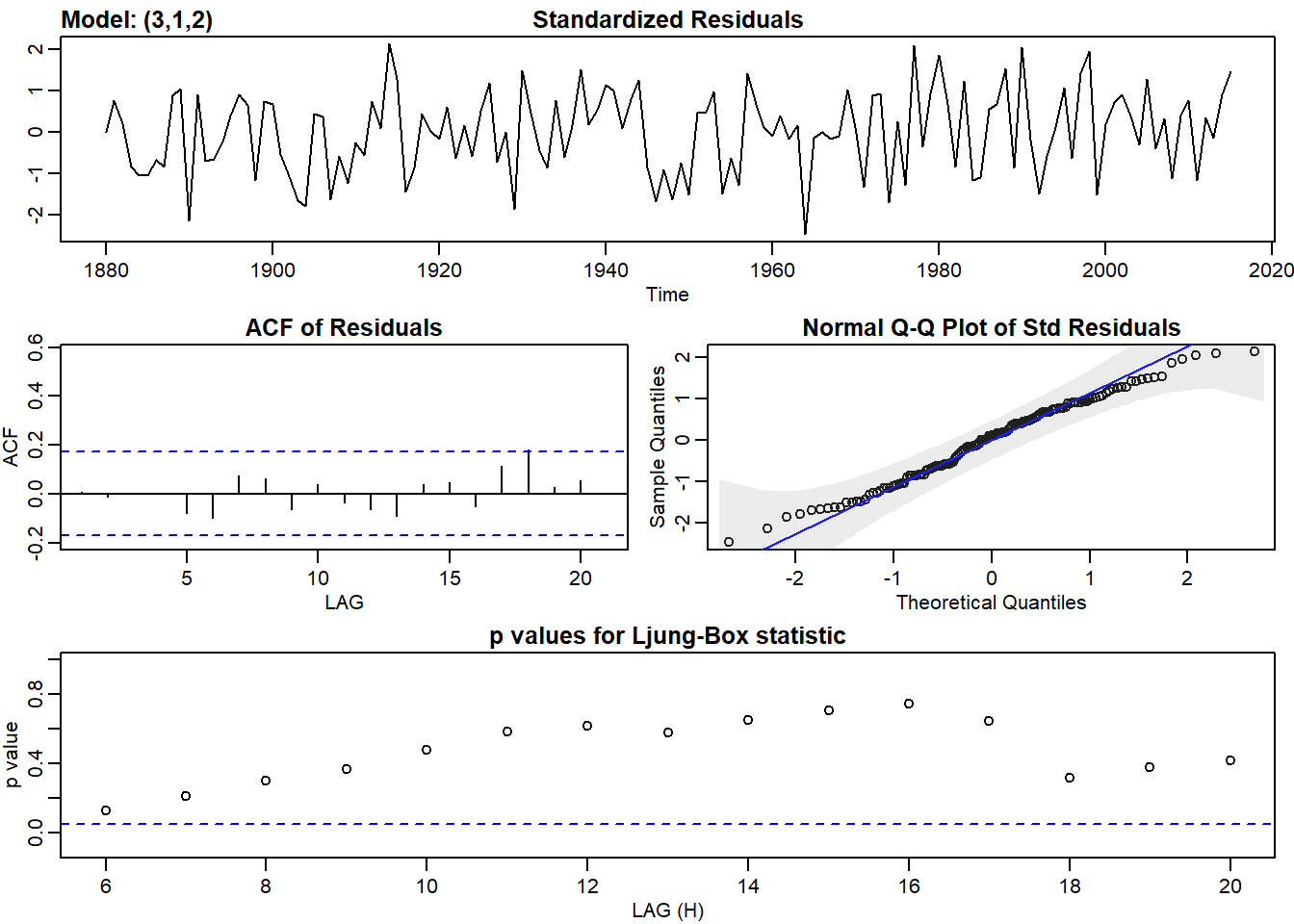
Ahora ejecutamos auto.arima a ver que nos sale:
# modelo hecho automáticamente
auto.arima(globtemp, stepwise = FALSE)# con esto hacemos que trabaje mas el buscador de modelos## Series: globtemp
## ARIMA(1,1,3) with drift
##
## Coefficients:
## ar1 ma1 ma2 ma3 drift
## -0.9449 0.6081 -0.5680 -0.3091 0.0072
## s.e. 0.0562 0.0971 0.0856 0.0804 0.0032
##
## sigma^2 estimated as 0.009775: log likelihood=123.06
## AIC=-234.12 AICc=-233.47 BIC=-216.69Vemos que auto.arima propone un arima(1,1,3)
modelo2<-sarima(globtemp,1,1,3)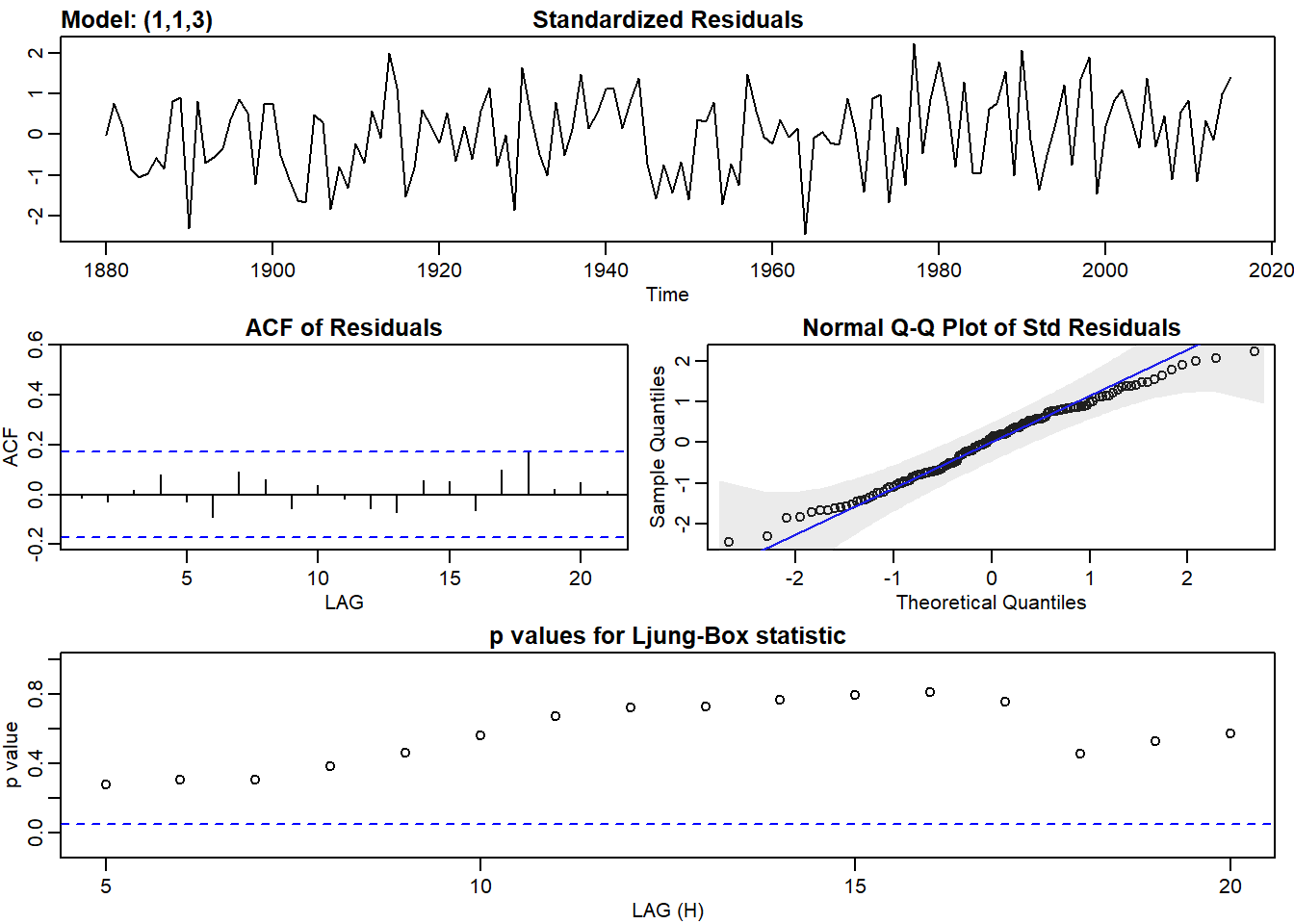
pro1<-sarima.for(globtemp, n.ahead = 20, p = 3, d = 1, q = 2)
pro2<-sarima.for(globtemp, n.ahead = 20, p = 1, d = 1, q = 3)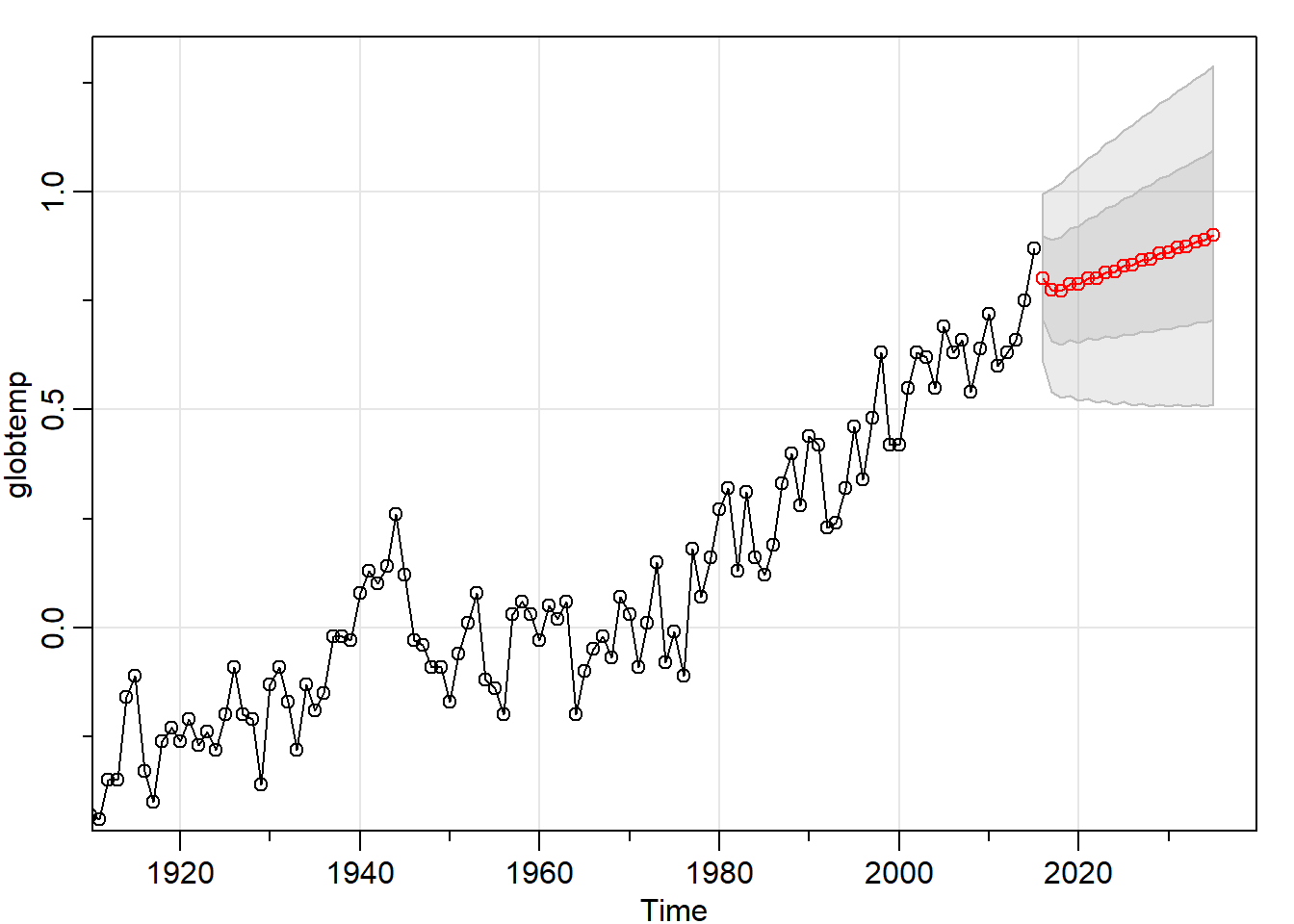
print(paste("AIC_arima(3,1,2)=",round(modelo1$AIC,2),"AIC_arima(1,1,3)=",round(modelo2$AIC,2)))## [1] "AIC_arima(3,1,2)= -1.72 AIC_arima(1,1,3)= -1.73" autoplot(globtemp) +ggtitle("Comparación modelos 1 y 2")+
#añadimos pronostico automatico
autolayer(pro1$pred)+
autolayer(pro2$pred)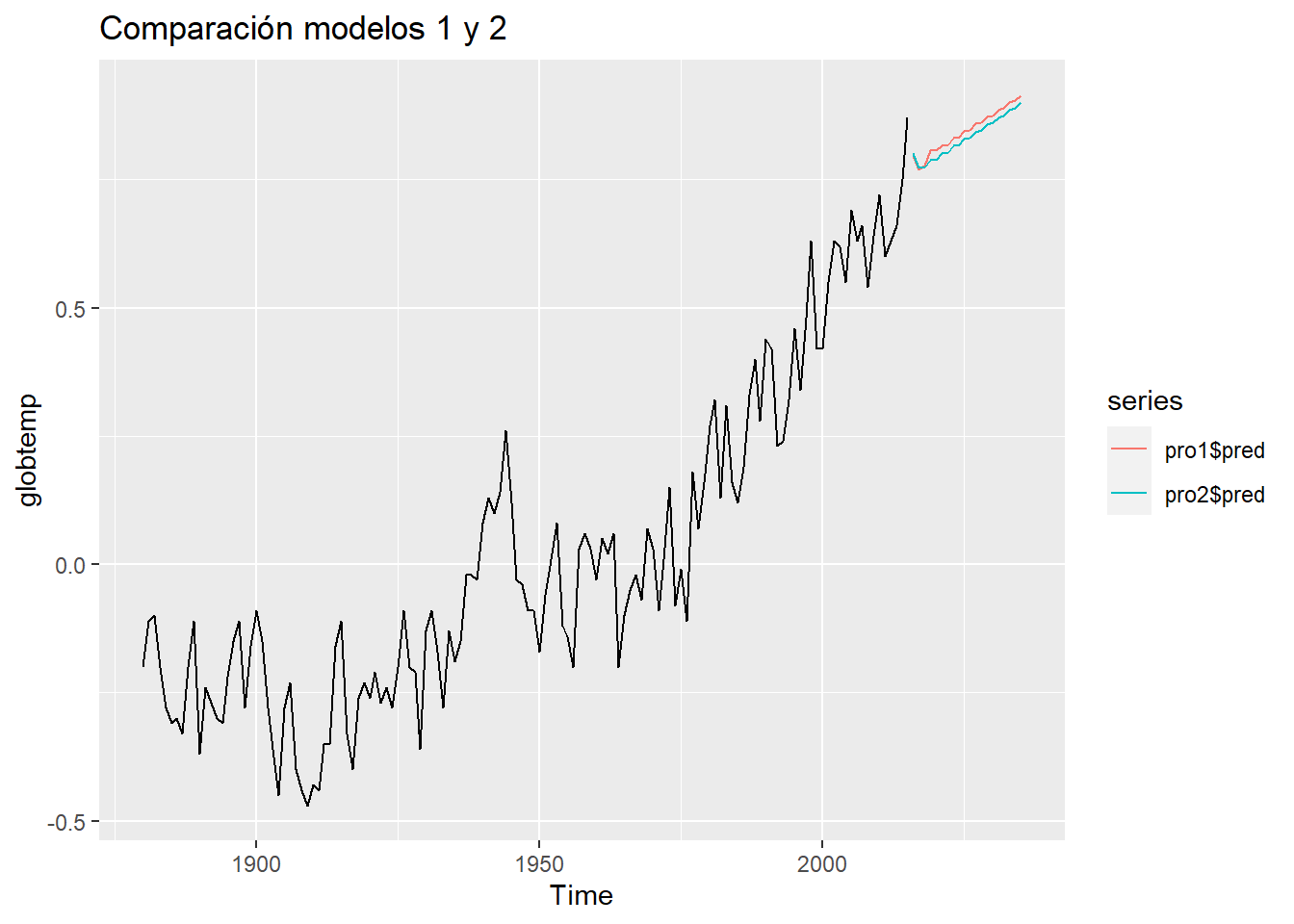
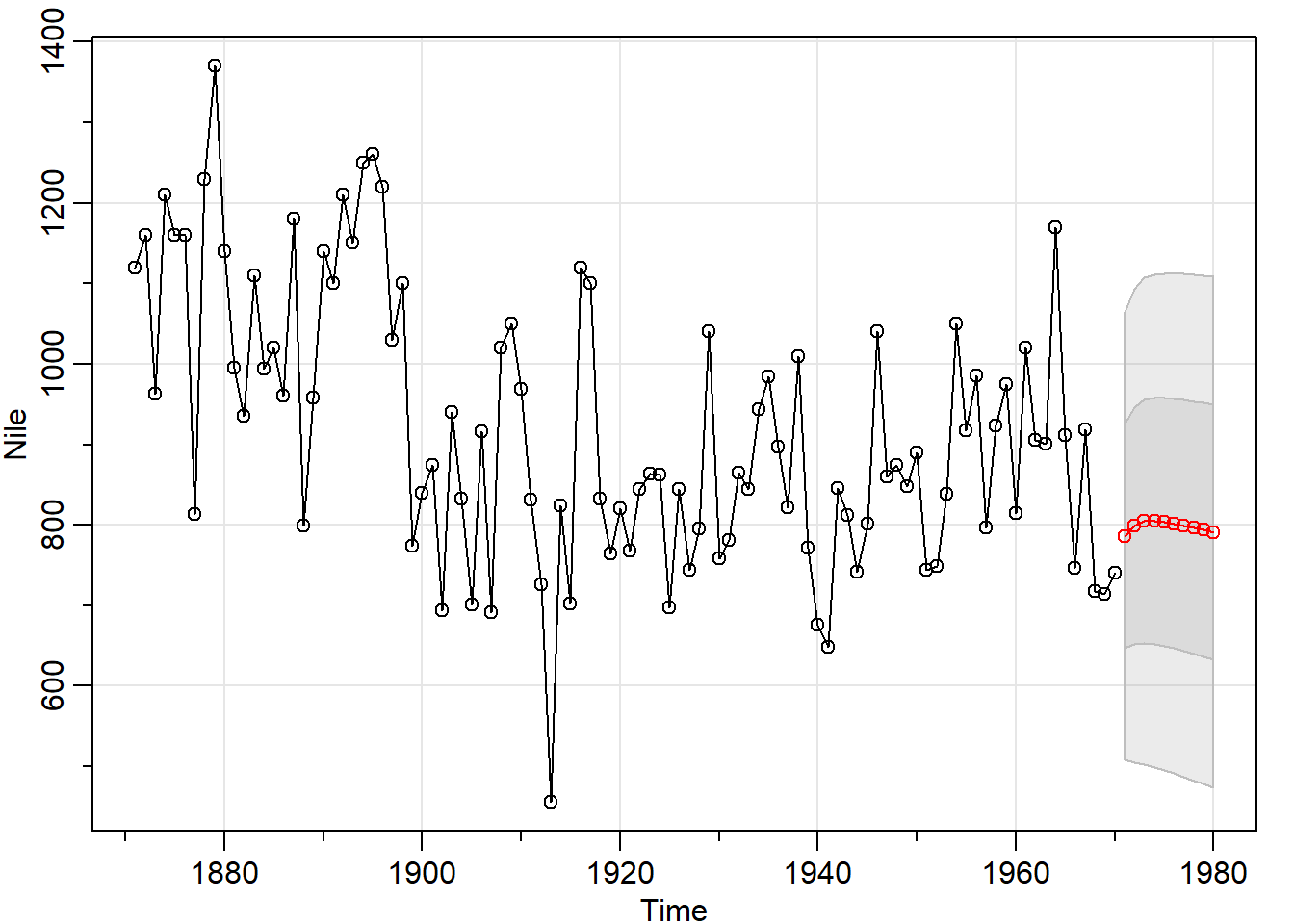
Ejemplo4. Caudales máximos del Nilo
Esta serie contiene los caudales máximos del río Nilo anulales desde 1871 a 1970.
# vemos qué contiene Nile
periodicity(Nile)## Yearly periodicity from 1871-01-01 to 1970-01-01# las gráficas
ggtsdisplay(Nile)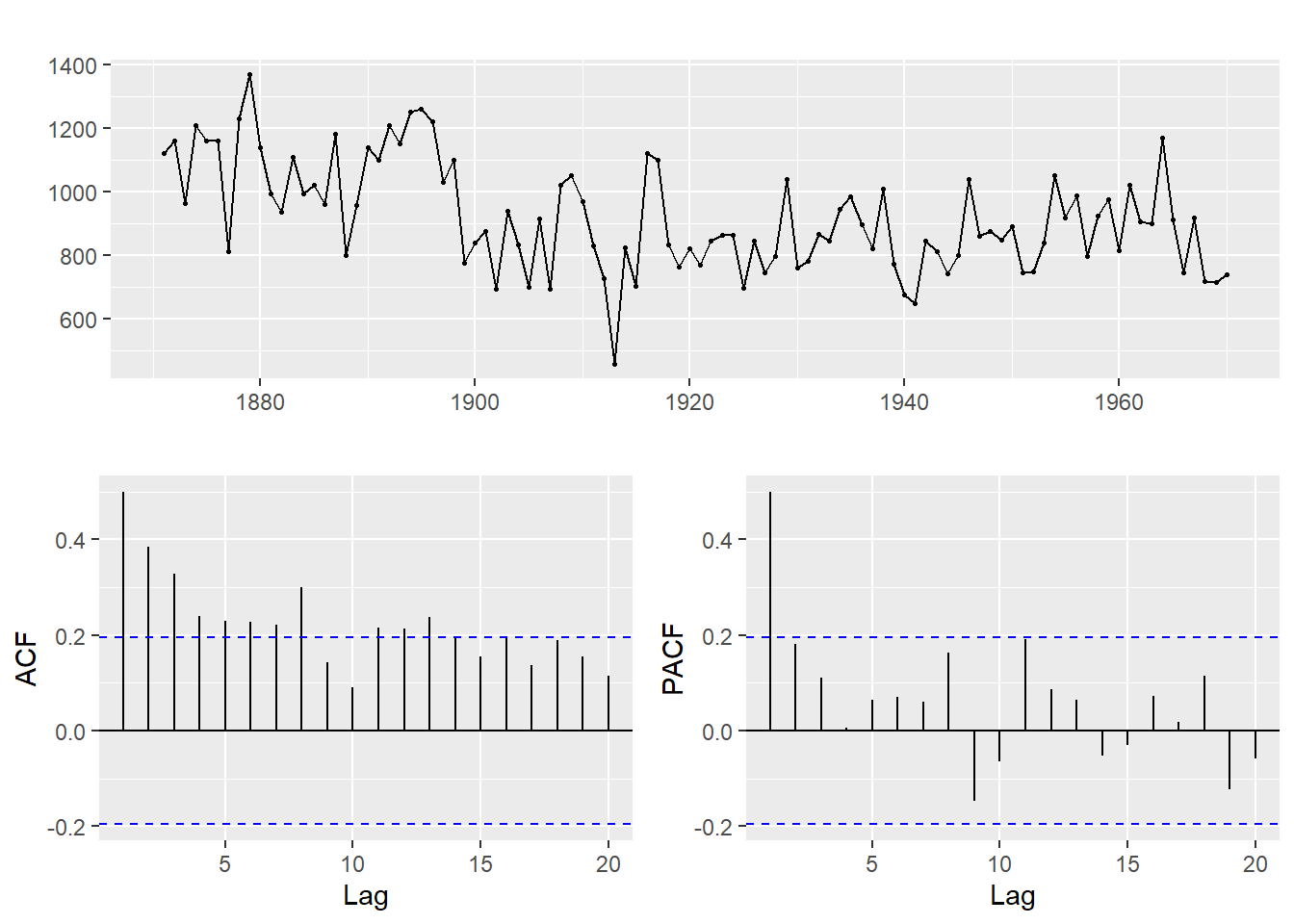
# calculamos las diferencias básicas y estacionales
ndiffs(Nile)## [1] 1#nsdiffs(Nile)
ggtsdisplay(diff(Nile))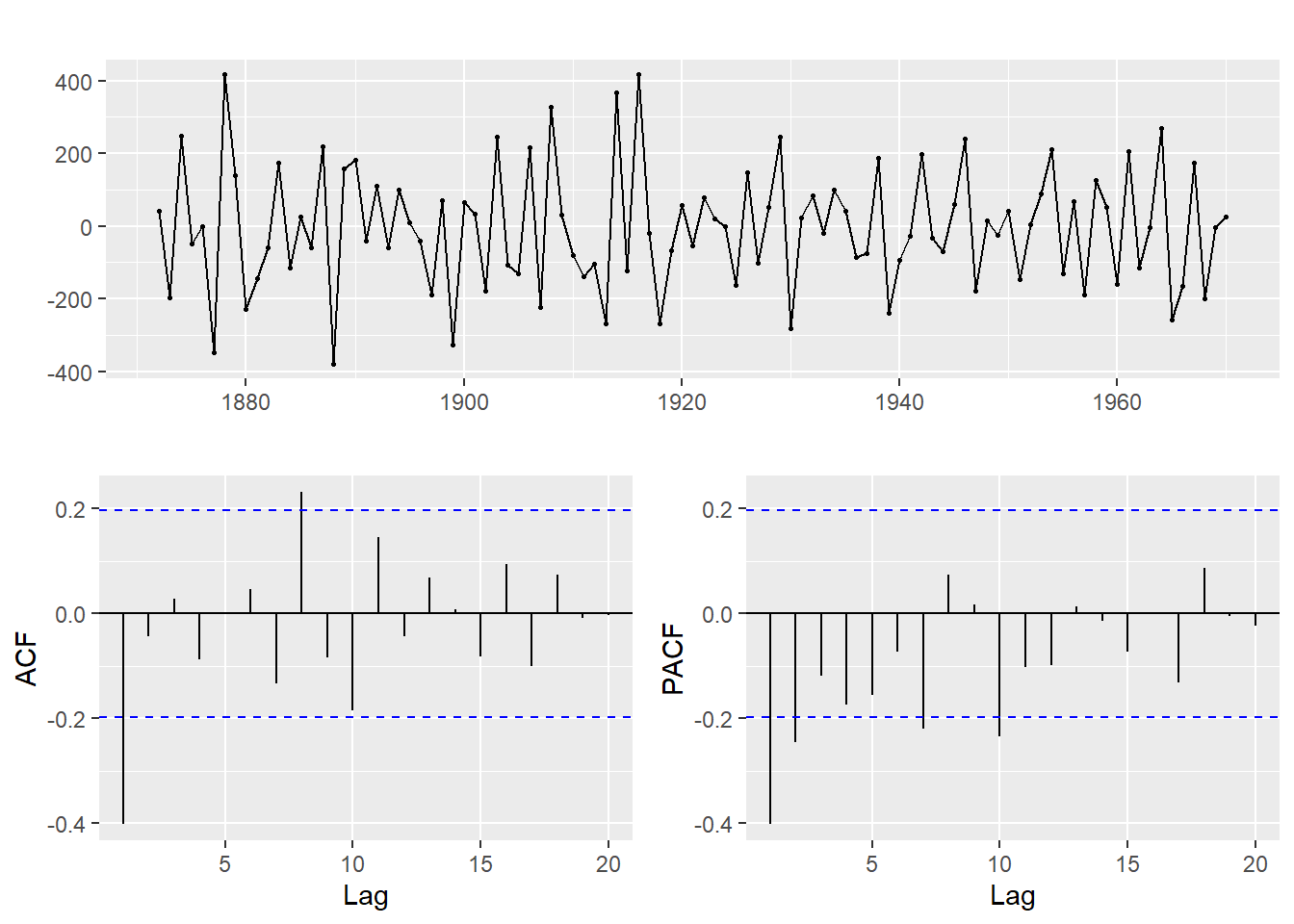 La serie parece tener tendencia a la baja, que se confirma con
La serie parece tener tendencia a la baja, que se confirma con ndiffs=1. No hay ciclos estacionales y tampoco vemos claramente una varianza heterogenea, por lo que no hacemos transformación de la serie.
De las gráficas y correlogramas de diff(Nile), se deduce que un modelo puede ser el arima(2,1,1), al tener la ACF un valor inicial significativo y la PACF 2.
Ejecutamos el modelo y vemos los residuos:
sarima(Nile,2,1,1)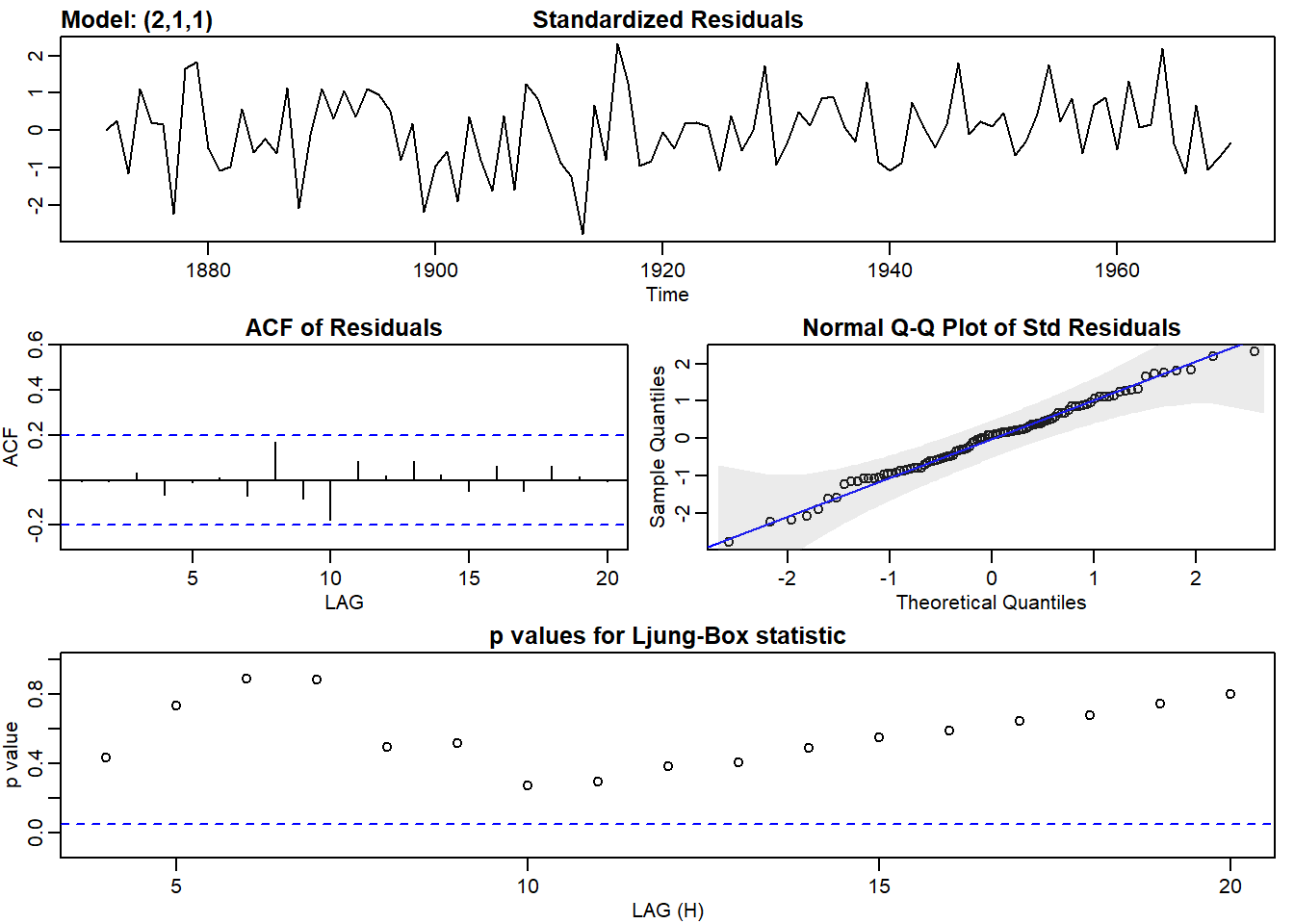
sarima.for(Nile,10,2,1,1)