Generación aleatoria
Generación de series aleatorias
A veces, necesitamos crear series de datos “inventados” para comprobar modelos, estudios o hipótesis. La generación aleatoria es un tema interesante y útil por lo que he recopilado en este artículo diferentes métodos sencillos que uso para crear series de datos “de la nada”.
Se trata de simples funciones de Rbase con las que podemos generar series aleatorias o secuencias con propiedades predefinidas, imprescindibles para validación de modelos.
Empecemos por lo básico:
función sample
Quizás la función más simple, potente y olvidada para generar una serie de datos aleatorios es sample(). Solo hay que indicarle como argumento el vector origen del que se extraen los datos (números, letras ..), después el número de elementos de la serie a generar y si se puede o no repetir elemento.
set.seed(123) # semilla de inicio
# No admite repeticiones:
sample(1:10, 5, replace = F)## [1] 3 10 2 8 6# Si admite repeticiones:
sample(LETTERS[1:3], 10, replace = T)## [1] "C" "A" "B" "B" "A" "B" "C" "A" "C" "C"En realidad estas funciones como sample generan lo que se denomina pseudoaleatoriedad, esto es, no son puramente aleatorias pero se parecen muchísimo. Además tienen una característica esencial y es que son reproducibles - con los mismos y exactos valores- si se parte de la misma semilla. Por esto, si queremos que otros comprueben los cálculos hay que aportar la semilla inicial, esto se con la función set.seed.
La función sample es muy útil cuando queremos generar números enteros de un conjunto predefinido, así:
vec<-c(3,24,77,91)
sample(vec,10,replace=T)## [1] 3 91 3 3 3 77 91 24 77 24O para crear una serie de letras o una serie binaria, combinando con la función ifelse:.
# generamos letras minusculas
sample(letters[2:16],10)## [1] "j" "o" "d" "e" "b" "h" "f" "m" "k" "c"# Generamos serie binaria 0/1
x1<-sample(1:10,20,replace=T)
# filtro con ifelse generamos una binomial
ifelse(x1>5,1,0)## [1] 1 1 1 1 1 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1Otra opción de sample interesante, es que se pueden asignar probabilidades a cada suceso, por lo que si queremos una serie binaria con un 20% de ceros y un 80% de unos lo haremos utilizando el argumento prob, así:
# serie con probabilidad dada
serie01<-sample(0:1, 20, replace=T, prob=c(0.2,0.8))
serie01## [1] 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1#resumen de resultados
table(serie01)## serie01
## 0 1
## 3 17Con este argumento es sencillo inventarse encuestas o series para ejercicios de estadística.
Función seq
La función seq(min, max, by, len) permite hacer secuencias de números y generar un vector con las características que le indicamos.
Es uno de los pilares básicos para crear cualquier serie aleatoria incremental o fechas espaciadas. Ten en cuenta que solo hacen falta 3 de sus 4 argumentos para generar la serie, por lo que se pueden definir de muchas formas jugando con con el valor mínimo, el máximo, la longitud total de la serie (len=) o el intervalo (by=) entre elementos.
# Creamos una serie de 0 a 10 de 5 en 5.
x <- seq(0,100,by = 5)
# secuencia de enteros
as.integer(seq(1, 80,length.out=12))## [1] 1 8 15 22 29 36 44 51 58 65 72 80# length.out=5 especifica la longitud de la serie
# pero podemos simplificarlo por len
seq(4,24,len=5)## [1] 4 9 14 19 24Secuencia de fechas
Con seq creamos también fechas espaciadas un mismo intervalo para crear series temporales, por ejemplo así:
# secuencia de fechas
ini=as.Date("31/05/2021", format="%d/%m/%Y")
seq(ini, by=2,len=5) # dias## [1] "2021-05-31" "2021-06-02" "2021-06-04" "2021-06-06" "2021-06-08" seq(ini, by="week",len=5) # semanal## [1] "2021-05-31" "2021-06-07" "2021-06-14" "2021-06-21" "2021-06-28" seq(ini, by="year",len=5) # anual## [1] "2021-05-31" "2022-05-31" "2023-05-31" "2024-05-31" "2025-05-31" seq(ini, by="quarter",len=5) ## [1] "2021-05-31" "2021-08-31" "2021-12-01" "2022-03-03" "2022-05-31" fin=as.Date("30/09/2021", format="%d/%m/%Y")
seq(from=ini,to=fin, by="week")## [1] "2021-05-31" "2021-06-07" "2021-06-14" "2021-06-21" "2021-06-28"
## [6] "2021-07-05" "2021-07-12" "2021-07-19" "2021-07-26" "2021-08-02"
## [11] "2021-08-09" "2021-08-16" "2021-08-23" "2021-08-30" "2021-09-06"
## [16] "2021-09-13" "2021-09-20" "2021-09-27" seq(from=ini,to=fin, len=12)## [1] "2021-05-31" "2021-06-11" "2021-06-22" "2021-07-03" "2021-07-14"
## [6] "2021-07-25" "2021-08-05" "2021-08-16" "2021-08-27" "2021-09-07"
## [11] "2021-09-18" "2021-09-30"Función rep
Otra función que nos permite hacer series es rep y sirve para repetir una secuencia varias veces.
secuencia<-c(1,3,7)
rep(secuencia,4)## [1] 1 3 7 1 3 7 1 3 7 1 3 7#misma forma de llamar la función:
rep.int(secuencia,4)## [1] 1 3 7 1 3 7 1 3 7 1 3 7rep_len(secuencia,12)## [1] 1 3 7 1 3 7 1 3 7 1 3 7rnorm y similares
Rbase dispone de varias funciones de generación aleatoria de números según algunas distribuciones estadísticas. Las más conocidas son runif() y rnorm(), pero existen unas cuantas más:
runif()genera números aleatorios uniformemente distribuidos entre 0 y 1, o entre los valores que especifiquemosrunif(100, min = 0, max = 50)*rnorm(n, mean = 0, sd = 1)genera números aleatorios que siguen la distribución normal de media y desviación estándar dada.rbinom(n, size = 100, prob = 0.5)genera números aleatorios discretos binomiales. Esta distribución indica el éxito de experimentos aleatorios de éxito/fracaso (solo dos opciones). La función de distribución binomial especifica el número de veces que puede ocurrir un evento en un número independiente de tiradas dado porsizey dondeprobes la probabilidad de la ocurrencia del evento en una simple tirada.rpois(n, lambda = 4), Poisson es otra distribución de números discretos que se usa en experimentos de colas de tiempo.rexp(n, rate = 1)o Exponencial es una distribución que expresa el tiempo entre eventos en un proceso de Poisson.rgamma(n, shape = 1)genera números según la distribución gamma. Puede ser interesante ya que muchos procesos naturales siguen este tipo de distribución.
Usar una u otra serie generadora dependerá del objetivo que persigamos, a modo de ejemplo y para ver gráficamente las diferencias entre las funciones de distribución vamos a crear algunas series.
Juntaremos los datos en una tabla y representaremos gráficamente los histogramas para comparar y apreciar mejor estas diferencias.
#library(patchwork) # para pintar juntas las graficas
library(ggplot2)
library(cowplot) # formato de ggplot
library(reshape2) # para unir colum tabla
n=1000 # num de elementos generados
# variable x
ini=as.Date("07/07/1993", format="%d/%m/%Y")
x<- seq(ini, by=1,len=n) # dias
# generamos las variables y
y_nor<-rnorm(n, mean = 0, sd = 2)
y_uni<-round(runif(n,-10,10))
y_bin<-rbinom(n, size = 10, prob = 1/2)
y_exp<-rexp(n, rate = 1)
y_poi<-rpois(n, lambda = 5)
y_gam<-rgamma(n, shape = 1)
# unimos todo en un data frame y pintamos las series generadas
df<-data.frame(x,y_nor,y_uni,y_bin,y_exp,y_poi,y_gam)
df1<-melt(df , id.vars = 'x', variable.name = 'series')
ggplot(df1, aes(x,value)) + geom_line(aes(colour = series))+facet_grid(series ~ .)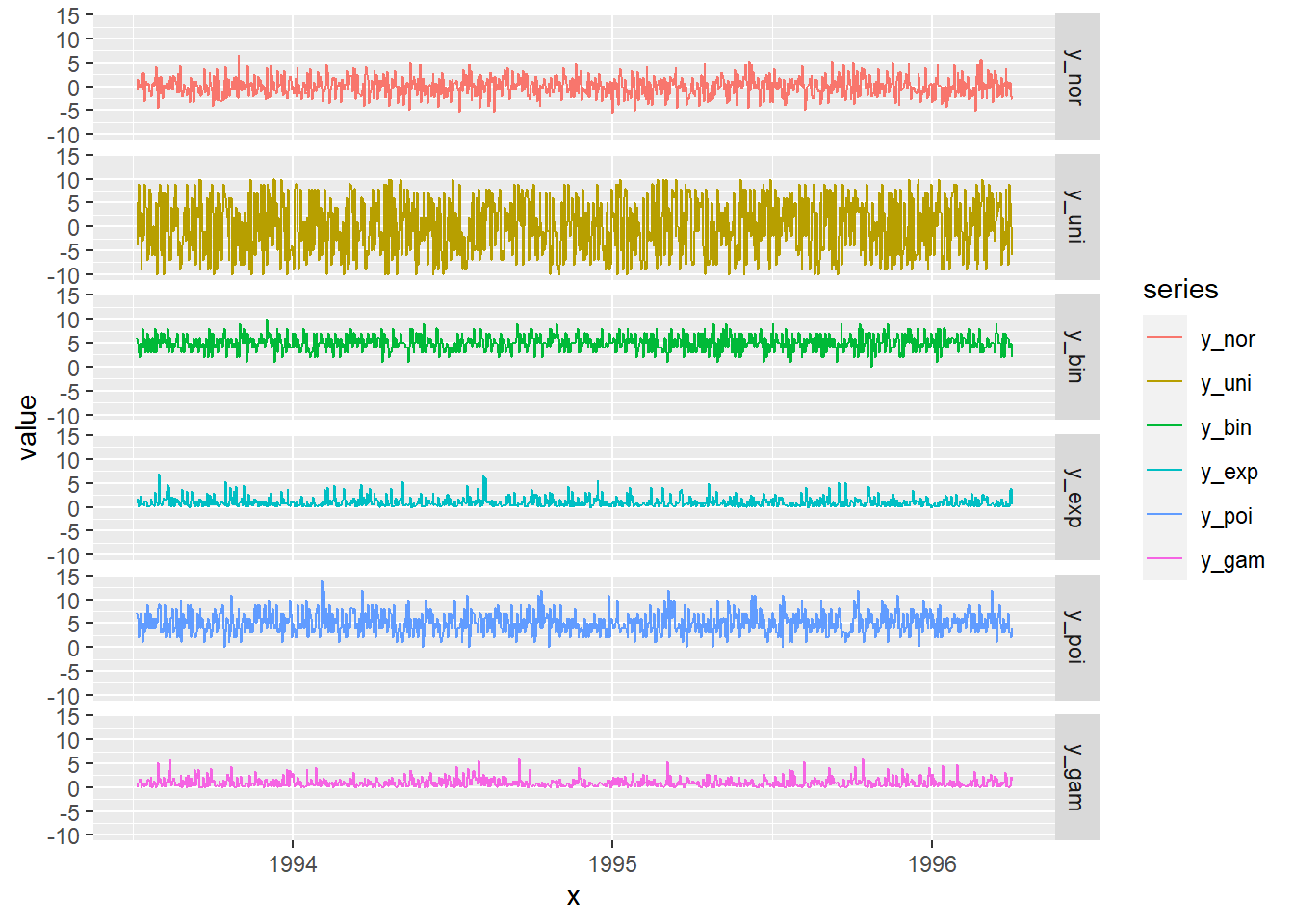
# pintamos los histogramas para apreciar mejor las diferencias
p1<- ggplot(df1, aes(x=value, fill=series))+
geom_histogram(binwidth =1,alpha=0.6,colour="black", position = 'identity') +
facet_wrap(vars(series))+
theme_cowplot(8)
p1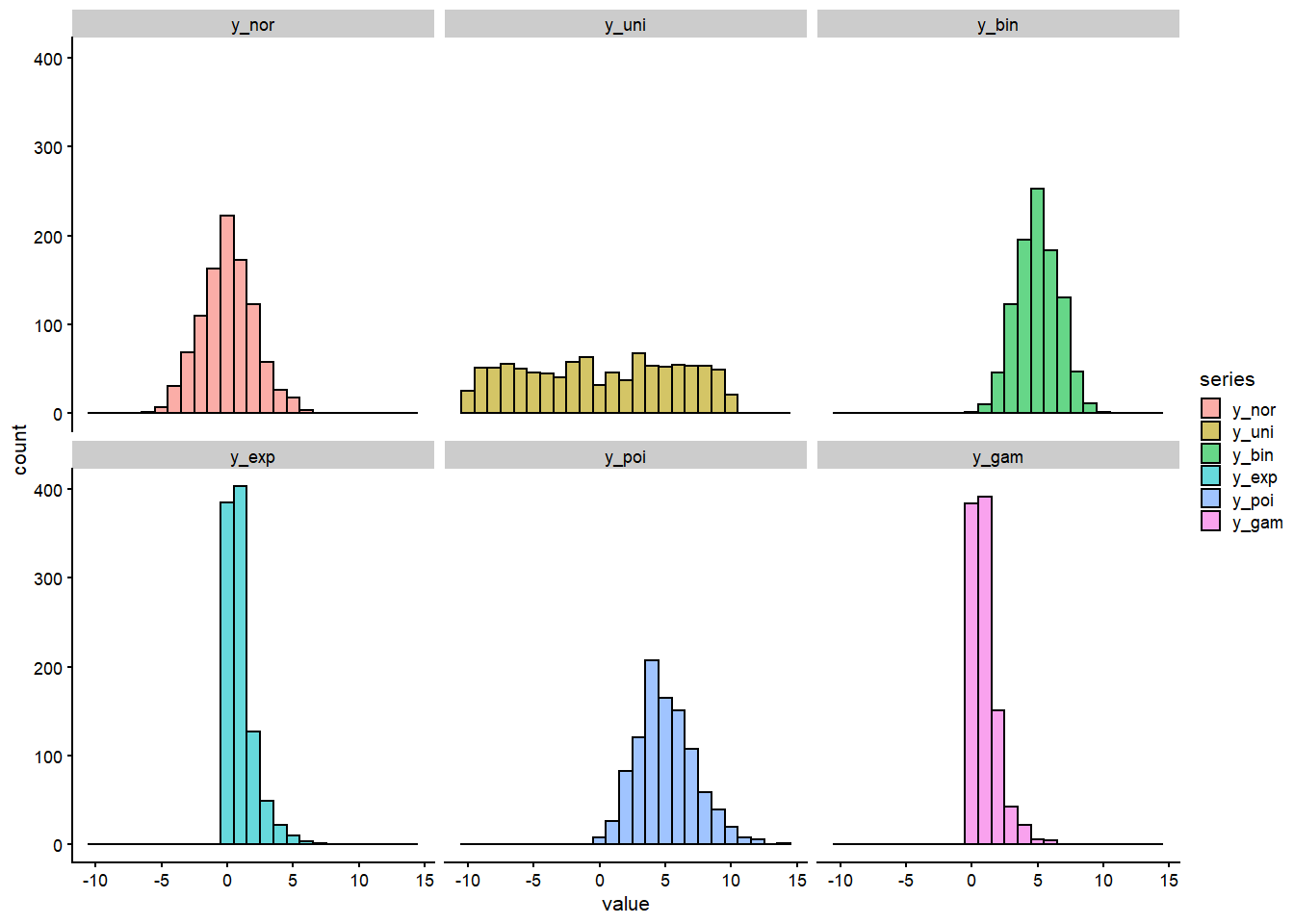
Las diferencias son claras a simple vista, y aunque no entramos en profundidad podemos intuir que cada una sirve para usos distintos. Las series aleatorias con estas funciones nos dan infinitas posibilidades, algunas funciones generan solo números positivos, otras tanto positivos como negativos, unas son uniformes en el rango mientras otras tienen un máximo centrado con más o menos inclinación a punta. Conocer el significado y explicación teórica de cada de estas distribuciones estadísticas es lo recomendable para saber en qué situaciones pueden usarse por lo que haremos un artículo en el futuro con casos prácticos realistas.
Por ejemplo, puedes usar Poisson para crear una serie de eventos en el tiempo, como los días de lluvia en un periodo.
library(xts)
# Generamos lluvia aleatoria entre dos fechas
# variable x fechas invierno 21
ini=as.Date("01/01/2021", format="%d/%m/%Y")
fin=as.Date("31/03/2021", format="%d/%m/%Y")
x<- seq(ini,fin, by=1) # dias
# serie de lluvias con poisson y norm
y<-rpois(length(x), lambda = .1)*rnorm(length(x),mean = 30, sd = 18)
lluviaDiaria<-xts(y,order.by=x)
autoplot(lluviaDiaria)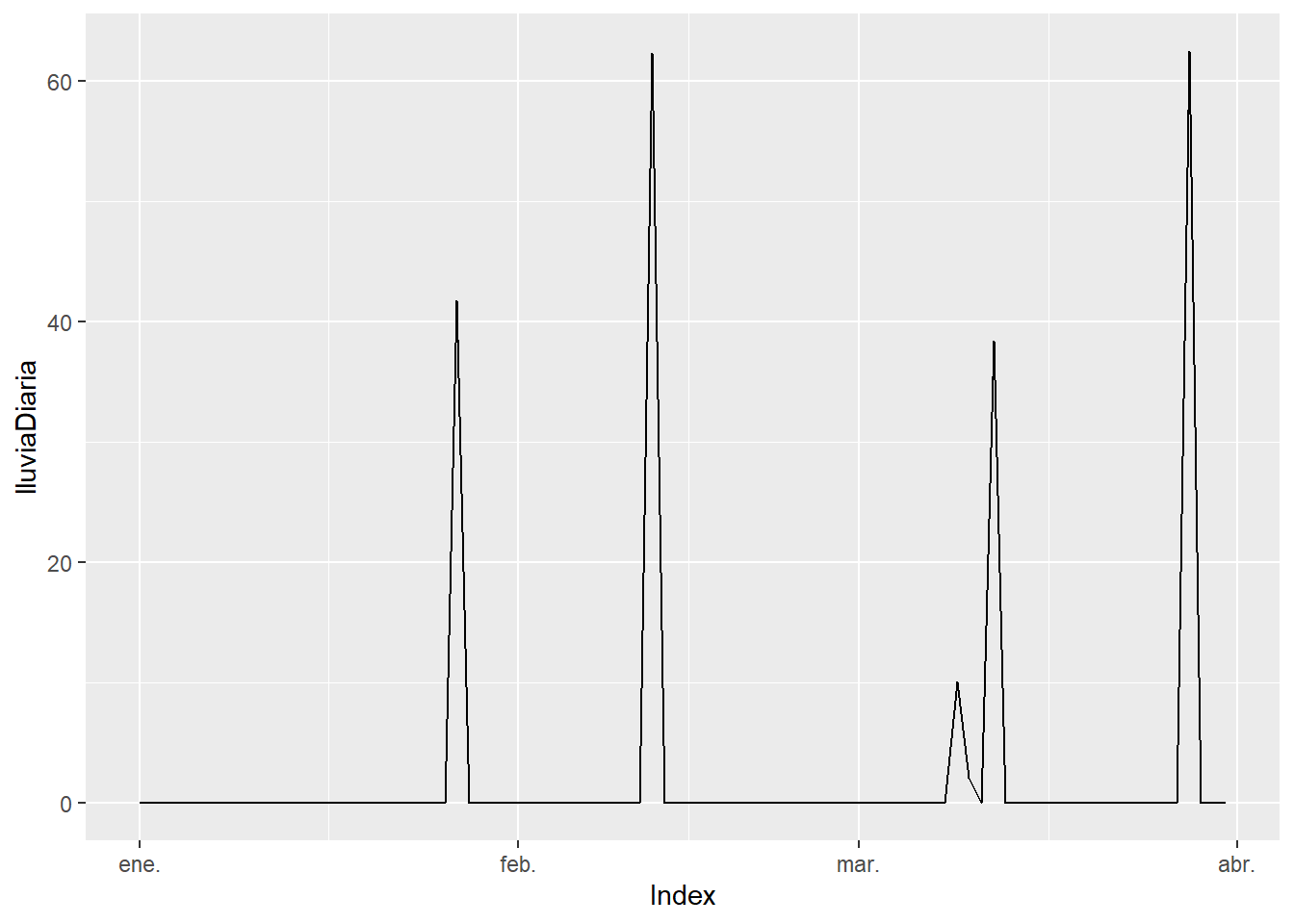
# creamos otra vista de la serie en calendario
library(calendR)
calendR(#year = 2021,
start_date = ini, # Custom start date
end_date = fin,
start = "M",
subtitle = "Dias de lluvia",
special.days = y,
gradient = TRUE,
special.col = rgb(0, 0, 1, alpha = 0.3),
low.col = "white",
weeknames.size = 4,
months.size=8) 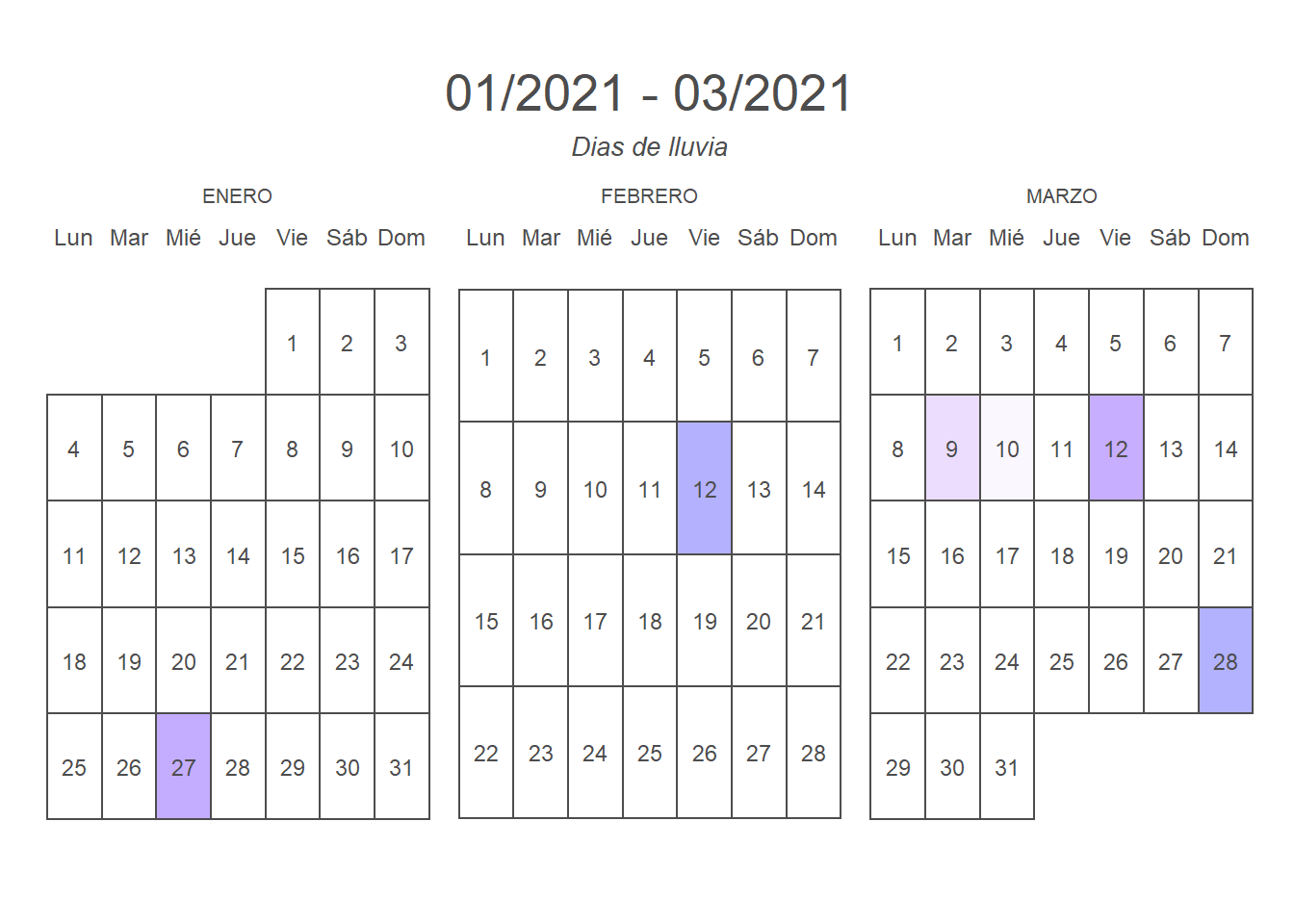
Las posibilidades gráficas de R son inmensas, ya has visto como podemos pintar un calendario, veamos alguna otra opcion de ver las series generadas como por ejemplo la vista matricial de los datos con la función ìmage`.
set.seed(7777)
n=400
s5<-ifelse(rgamma(n, shape = 1)>0.5,1,0)
# imagen matriz
image(matrix(s5,20,20),
col=c("white","darkred"),axes = FALSE, asp=1/1)
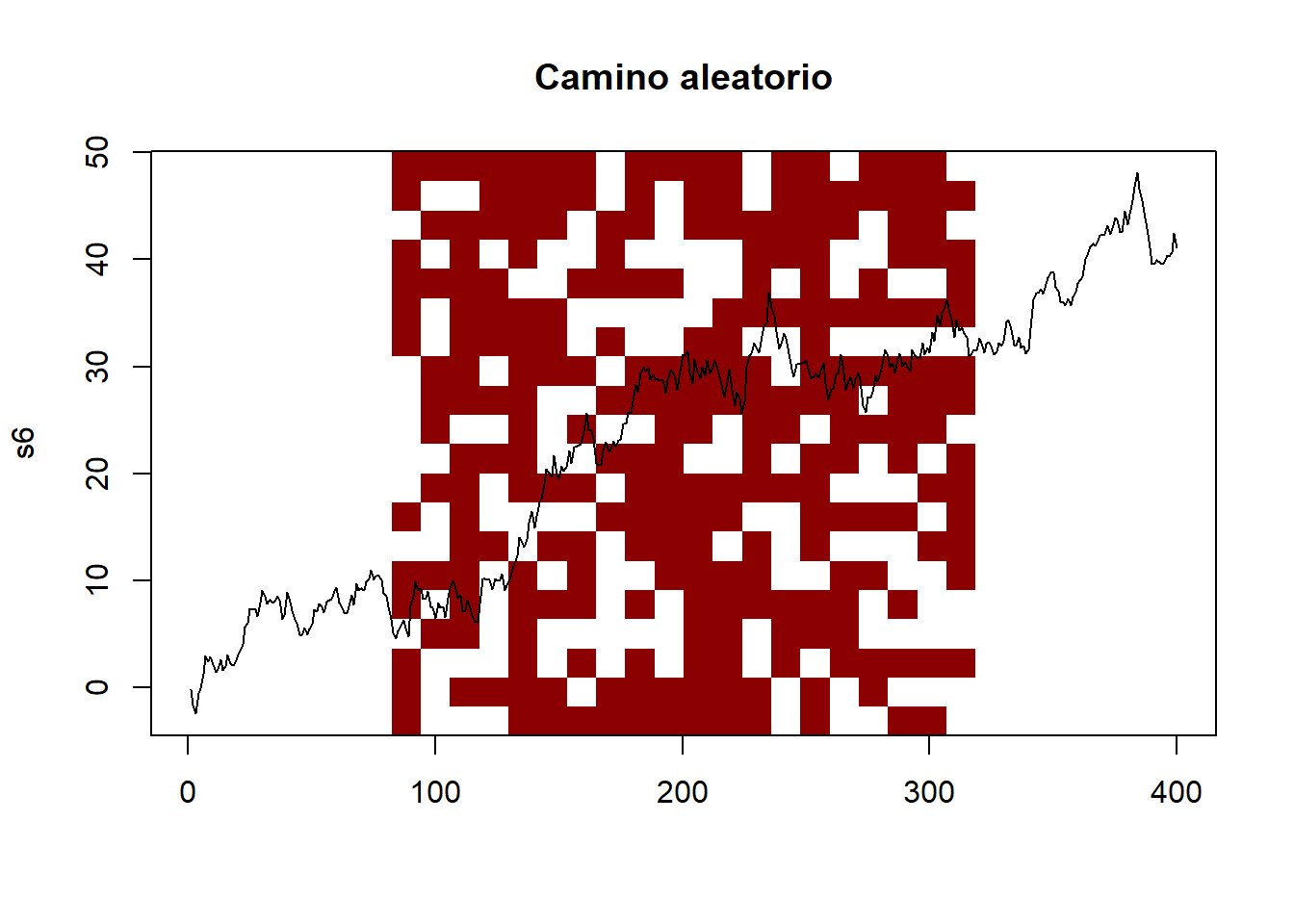
s6<-cumsum(rnorm(n))
plot(s6,type="l", main="Camino aleatorio",xlab="")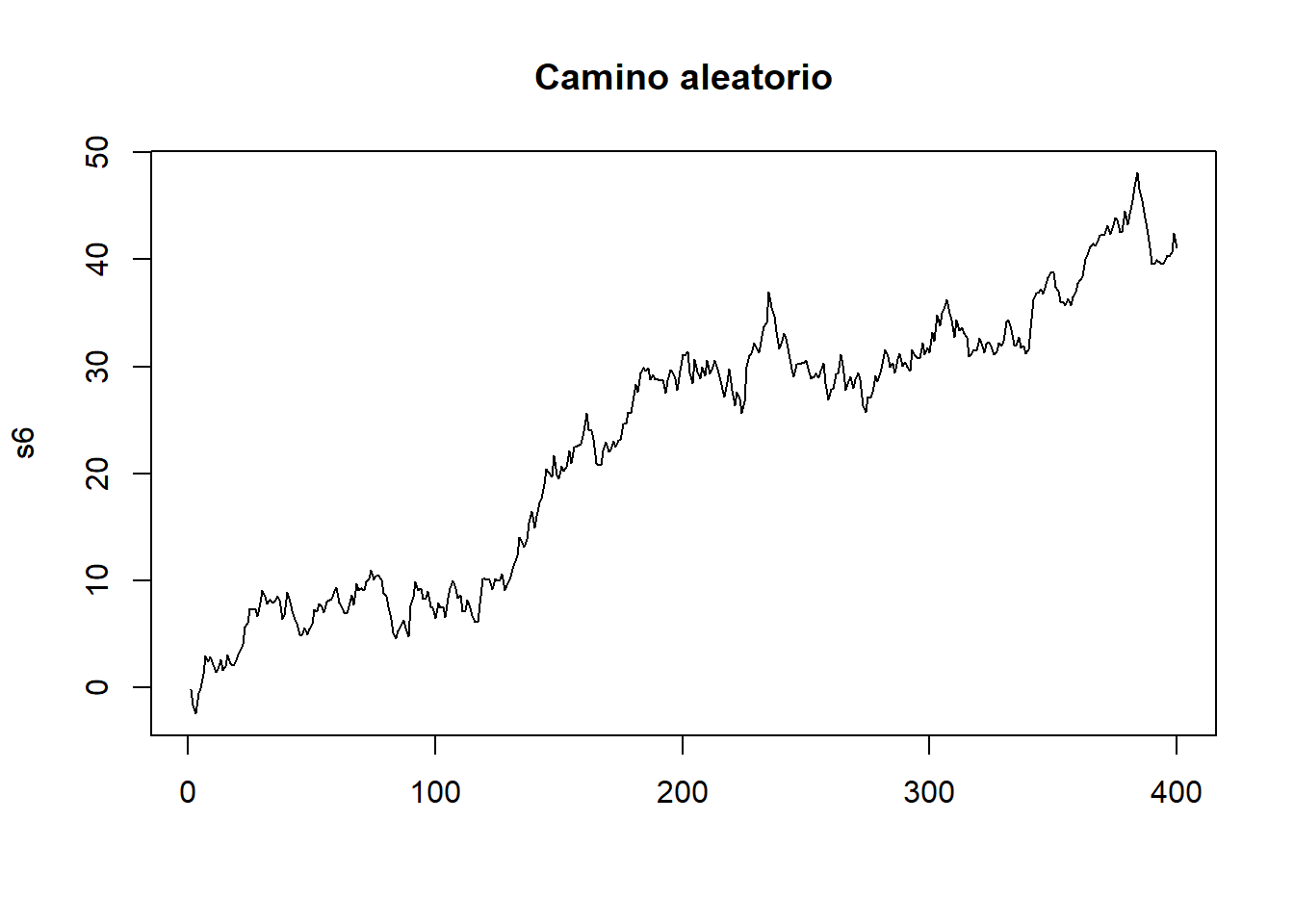
image(matrix(s6,20,20),
col=c(1:10),axes = FALSE, asp=1/1)
Series ARIMA
La funcion arima.sim también de Rbase es otra que nos sirve para generar series aleatorias, en este caso usando los procesos autoregresivos de ARIMA lo que abre un abanico inmenso siempre que conozcas el significado de cada orden (p,i q) de las ARIMA. Esto lo vimos en detalle en este post series temporales con ARIMA 1 y series temporales con ARIMA 2.
Con ARIMA generamos paseos aleatorios, ruido blanco y multitud de otras series combinando parámetros de cada uno de los órdenes.
set.seed(555)
# usamos la funion arima.sim de Rbase para generar
# Ruido blanco order=c(0,0,0)
plot(arima.sim(model=list(order=c(0,0,0)),n=100),ylab="", main="Ruido blanco")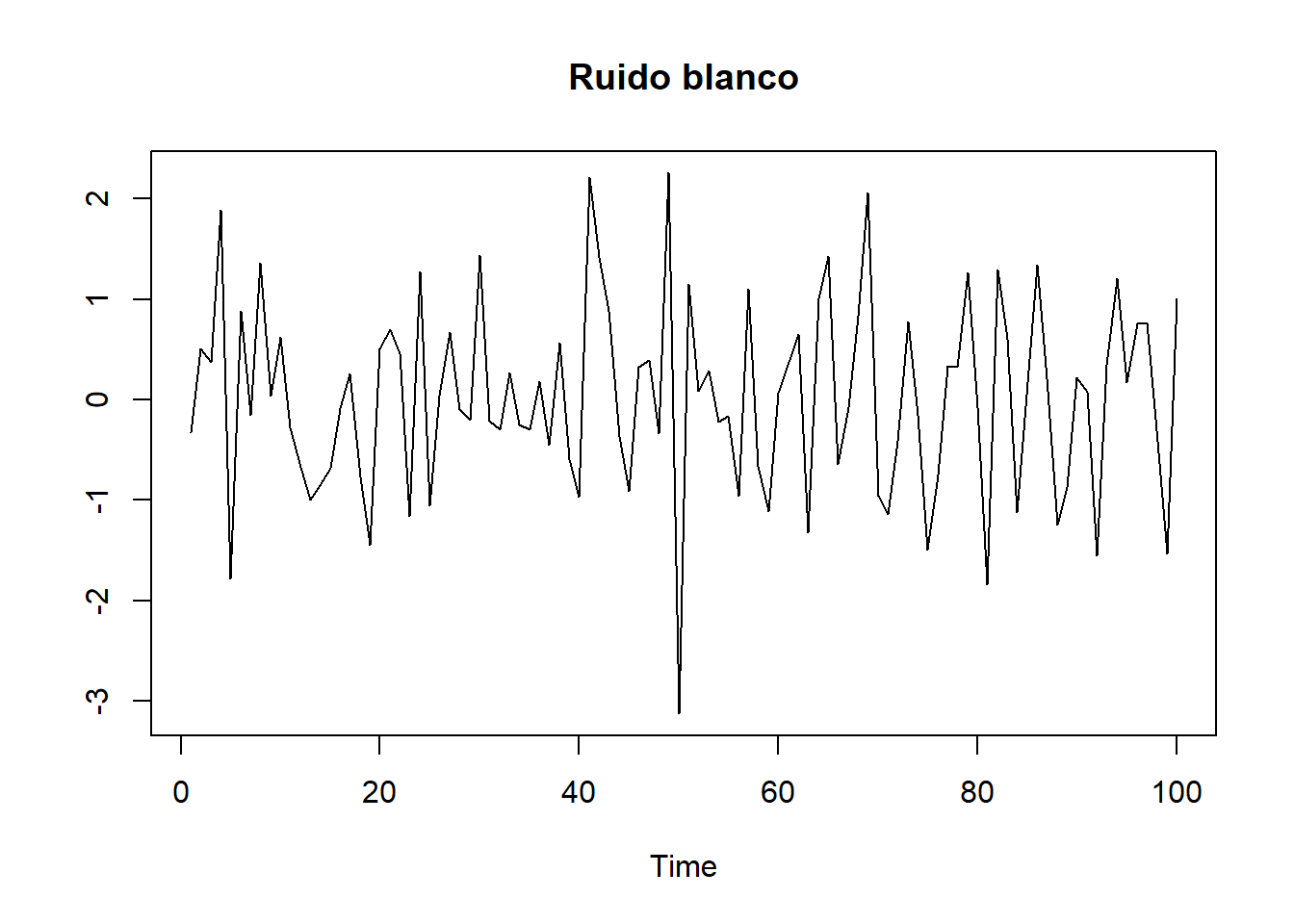
# Camino aleatorio order=c(0,1,0)
plot(arima.sim(model=list(order=c(0,1,0)),n=100),ylab="", main="Camino aleatorio") 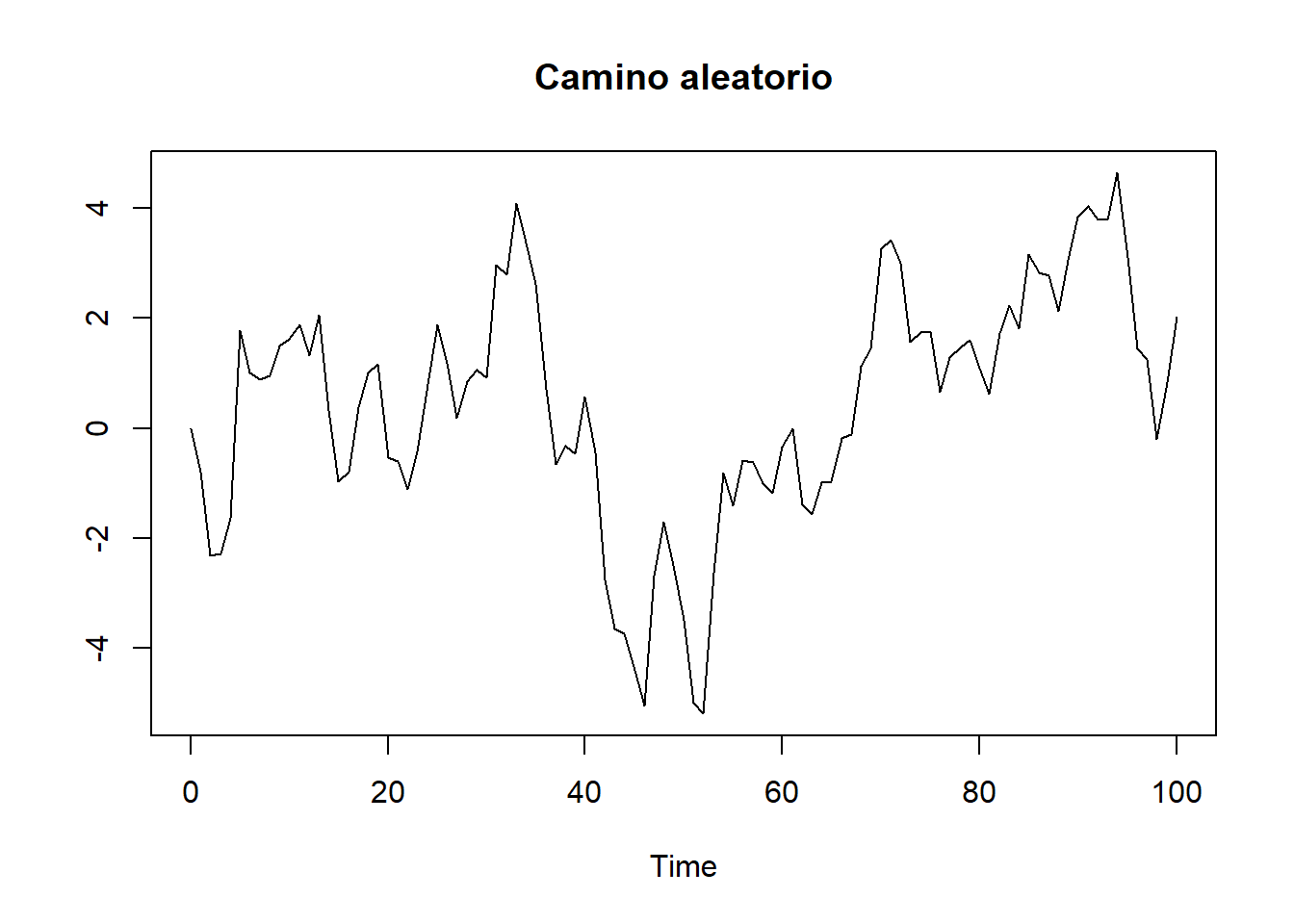
# añadimos fecha como x,en una serie mensual de valores
ini=as.Date("1/01/2000", format="%d/%m/%Y")
x<-seq(ini, by="months",length.out=48)
y<-arima.sim(model=list(order=c(0,1,0)),n=47)
plot(x,y,type="l",main="Serie camino aleatorio mensual", xlab="Fecha")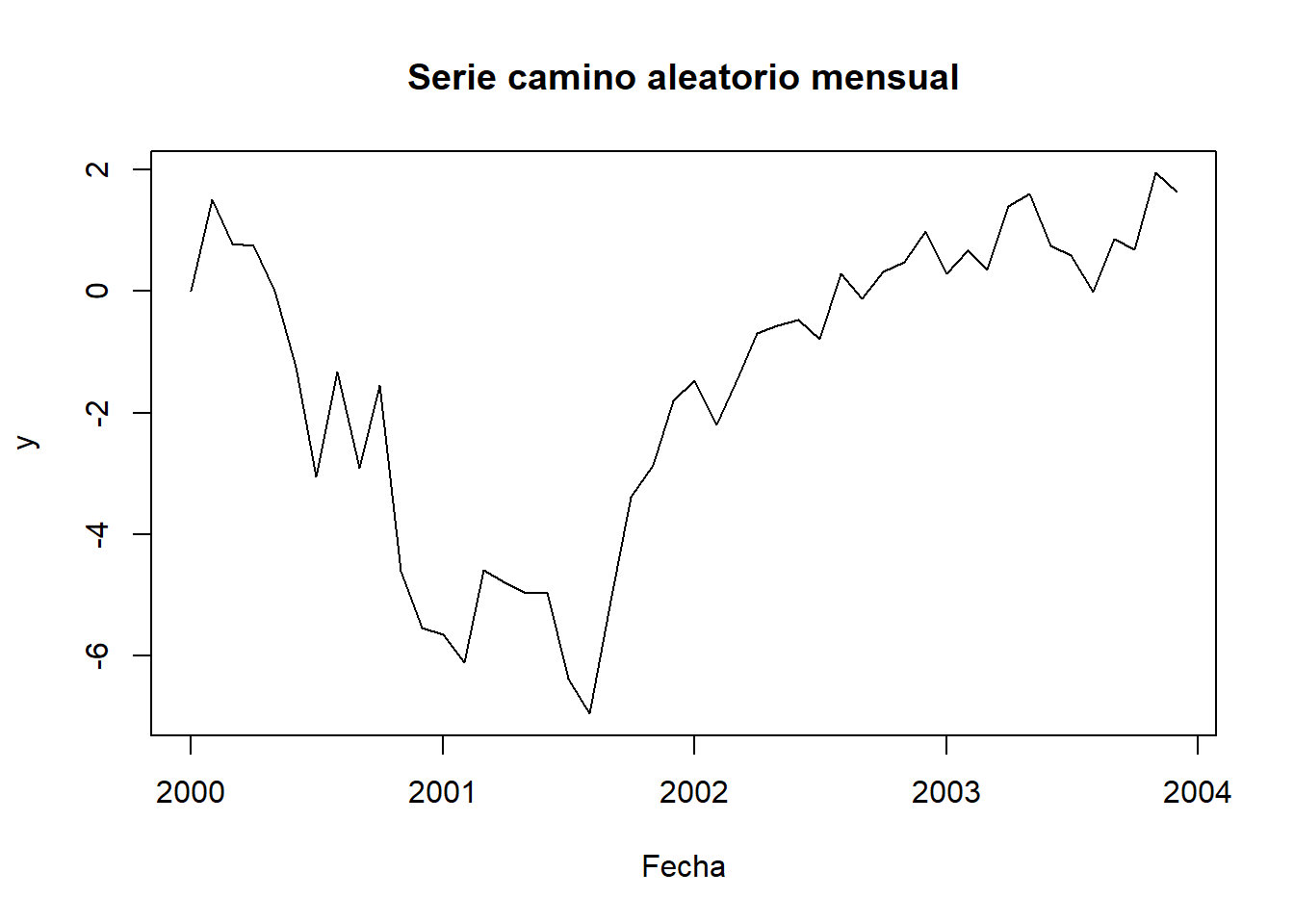
#y1<-xts(y,order.by=x)
# Otros casos de ejemplo
n=1000 # numero de valores a generar
ini=as.Date("1/01/2000", format="%d/%m/%Y")
x<-seq(ini, by=1,len=n+1) # +1 por i=1 orden diff
y<-100+arima.sim(model=list(order=c(0,1,2),ma= c(2,-0.5)),n)
plot(x,y,type="l",main="Evolucion valor A",
xlab="", col="red")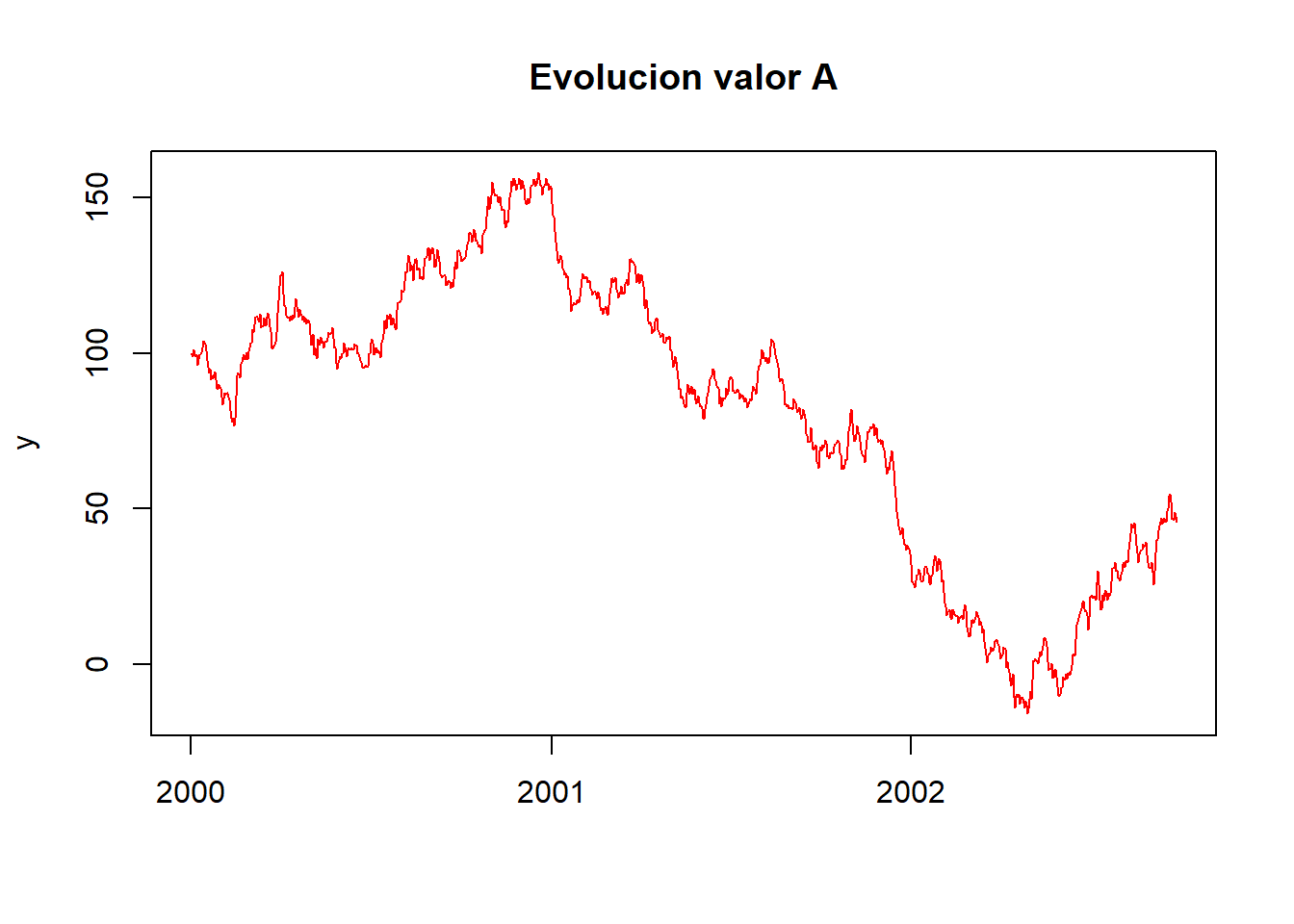
Ejemplo encuesta simulada
Por último veamos cómo crear los datos de una encuesta que necesitamos para un ejercicio de clase. Es interesante generar los datos nosotros porque así controlamos la forma de las variables resultado, y podemos interpretar mejor los futuros ejercicios que mandemos a los alumnos sobre la encuesta.
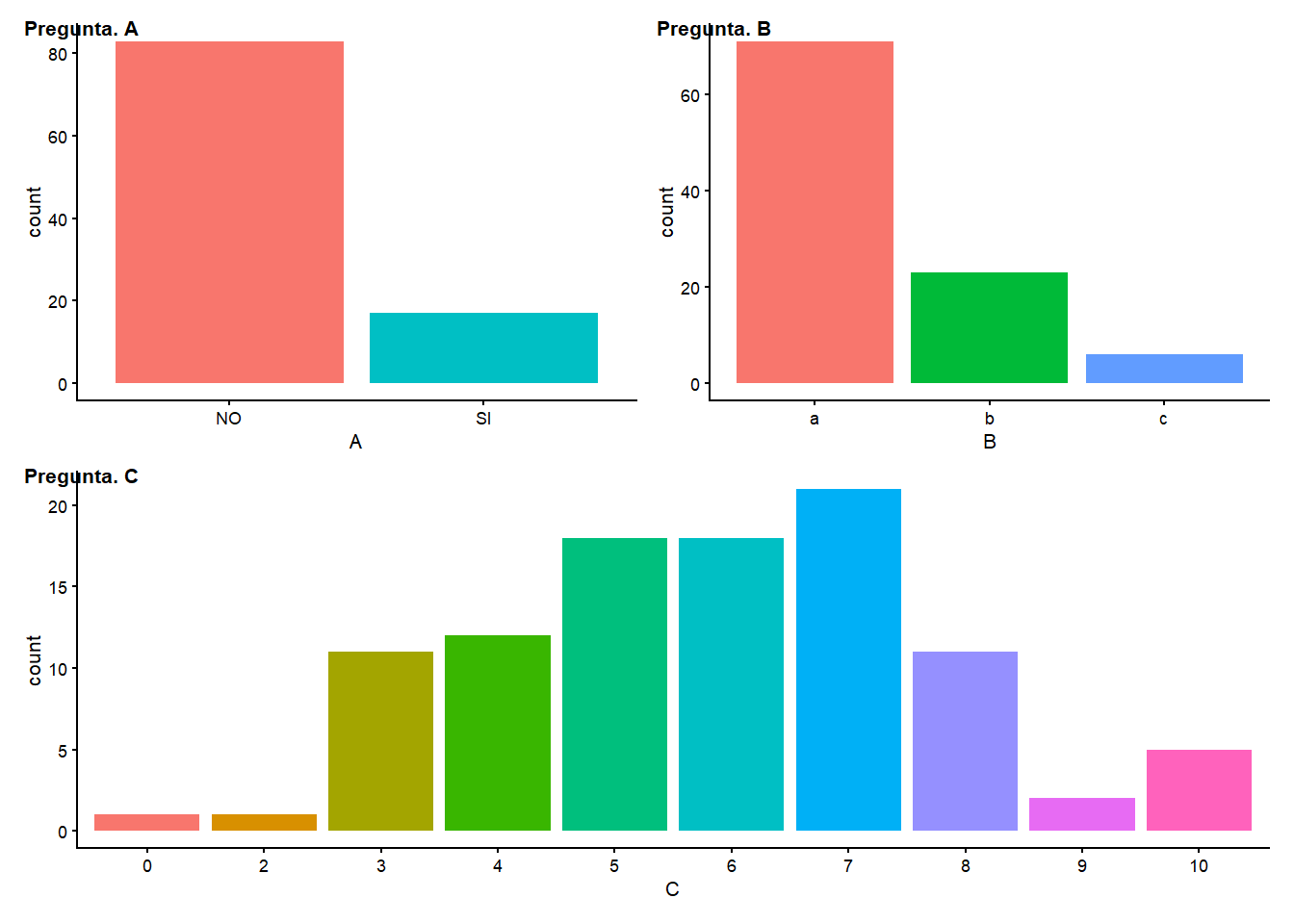
Vamos a imaginar que esta encuesta consta de 3 preguntas, que son:
- pregunta 1, respuestas posibles: SI/NO, con un 20% de probabilidad del SI y un 80% del NO.
- pregunta 2, con 3 posibles respuestas que clasificamos en a/b/c, con un 60/30/10 % de probabilidad de cada opción.
- pregunta 3, esta es una pregunta con respuesta gradual, una valoracion de 0 a 10, que queremos sea una normal con media 6 y solo admite numeros enteros.
El objetivo es generar una tabla final con un registro ( o fila) por cada usuario que haya respondido y una columna para cada respuesta de las 3.
Queremos generar una muestra de 100 encuestados, así que con estos datos empecemos:
library(patchwork) # para pintar juntas las graficas
n=100 # numencuestados
# creamos 3 series una para cada pregunta de la encuesta
# Pregunta A: Si/NO con 20% de SI
A<-ifelse(runif(n)>0.8,"SI","NO") # 1=si
A<-as.factor(A) # lo convertimos a factor
# creamos la tabla con la primera col
tabla_encuesta<-data.frame(A)
# Pregunta B: 3 respuestas posibles 3 prob
# usando sample para asignar prob a cada respuesta posible
B<-sample(c("a","b","c"),size=100,replace = T,prob=c(0.6,0.3,0.1))
tabla_encuesta$B<-as.factor(B)
# Pregunta C: valoracion de 0 a 10. entero
C<-round(rnorm(n,6,2))
C<-ifelse(C>10,10,C) # comprobamos que no sea > de 10
# Añadimos la ultima respuesta
tabla_encuesta$C<-as.factor(C)
tabla_encuesta$id<-rownames(tabla_encuesta)
head(tabla_encuesta,10)## A B C id
## 1 NO b 5 1
## 2 NO a 5 2
## 3 NO a 3 3
## 4 NO a 6 4
## 5 SI a 6 5
## 6 NO a 5 6
## 7 SI a 8 7
## 8 NO a 8 8
## 9 NO a 3 9
## 10 NO b 8 10#Graficas de respuesta de la encuesta
p1<-ggplot(data=tabla_encuesta, aes(x=A)) +
geom_bar(aes(fill=A),show.legend = FALSE)+
theme_cowplot(8)
p2<-ggplot(data=tabla_encuesta, aes(x=B)) +
geom_bar(aes(fill=B),show.legend = FALSE)+
theme_cowplot(8)
p3<-ggplot(data=tabla_encuesta, aes(x=C)) +
geom_bar(aes(fill=C),show.legend = FALSE)+
theme_cowplot(8)
# grafica conjunta con patchwork
g_encuesta<-(p1 + p2) /p3
g_encuesta+ plot_annotation(tag_levels = 'A',tag_prefix = 'Pregunta. ')